1. Using the method of shells, find the volumes of the solids given by revolving the regions:
- (a) The region enclosed between
and . Rotate about the -axis. - (b) The region under the curve
for . Rotate about the line .
3. Consider the curve
- (a) Find the arc length of this curve.
- (b) Using the method of bands, find the surface area of the revolution about the
-axis.
For this problem, you can use the formulas
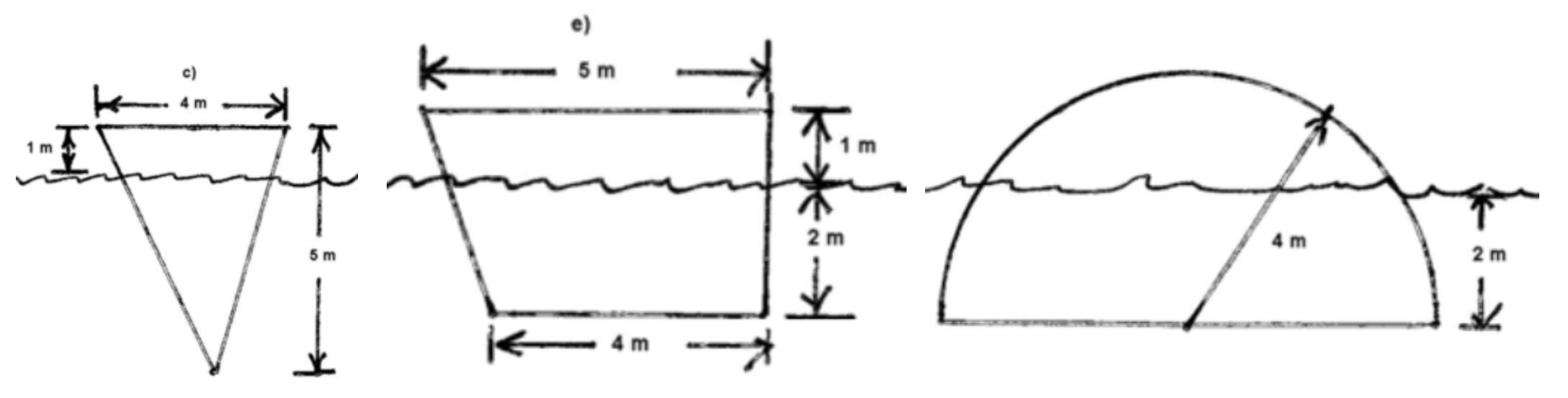
4. Set up the integrals that give the hydrostatic force on these shapes:
5. Find the CoMs of the regions:
(a) Area under the curve 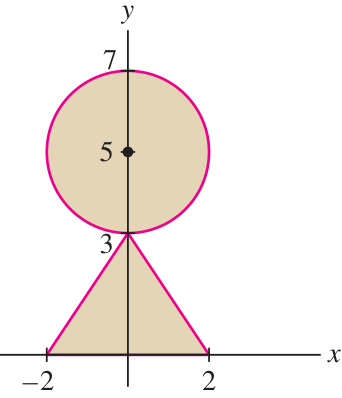
7. Set up an integral that computes the work done (against gravity) to build a circular cone-shaped tower of height
8. Use Simpson’s Rule with