Stepwise problems - Thu. 11:59pm
Shells
01
Shells volume - offset graph,
-axis Consider the region in the first quadrant bounded by the lines
, , , and the curve . Revolve this about the -axis. Find the volume of the resulting solid.
IBP
02
Integration by parts - A and E
Compute the integral:
03
Integration by parts - A and T
Compute the integral:
Regular problems - Sat. 11:59pm
Shells
04
Shells volume - set up integrals, both axes
Consider the region in the first quadrant bounded by the lines
and , and the curve . Set up integrals to find the volumes of the solids obtained by revolving this region about (i) the
-axis, and (ii) the -axis. (No need to evaluate these integrals.)
05
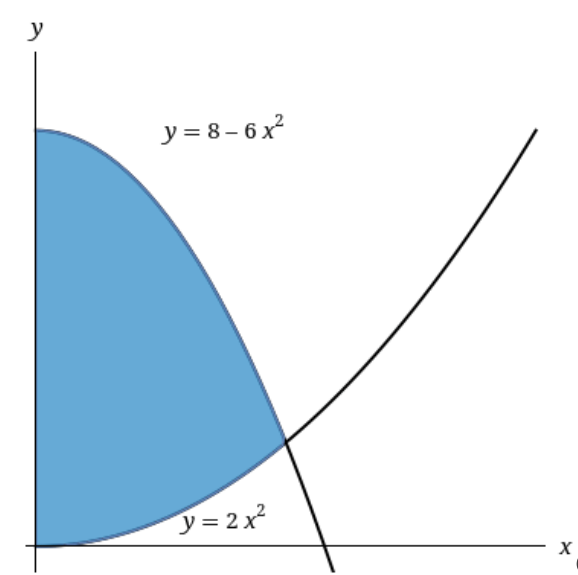
Shells volume - shells v. washers
Consider the region in the
-plane, in the first quadrant, bounded by the -axis on the left, by on the top, and on the bottom. A 3D solid is given by revolving this region around the
-axis.
- (a) Find the volume of the solid using the method of shells.
- (b) Attempt to find the volume of the solid using the method of washers/disks. Why is this harder? (TWO reasons!)
IBP
06
Integration by parts - A and L
Compute the integral:
07
Integration by parts - A and E
Compute the integral:
08
Integration by parts - A and I
Compute the integral:
09
Integration by parts - E and T, ‘breaking the circle’
Compute the integral:
You should perform IBP twice, find an equation, and use algebra to solve it (‘breaking the circle’) for the desired integral.