W04 - Examples

Transclude of Calculus-II---Examples---Unit-02#arc-length

![[Calculus II - Examples - Unit 02.md#Surface areas of revolutions - thin bands

12 - Arc length of chain, via position

A hanging chain describes a catenary shape. (‘Catenary’ is to hyperbolic trig as ‘sinusoid’ is to normal trig.) The graph of the hyperbolic cosine is a catenary:

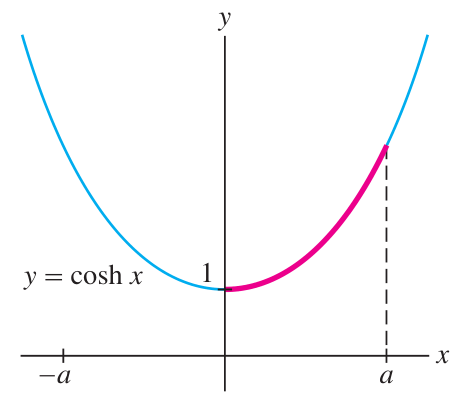
Let us compute the arc length of this catenary on the portion from to .

Solution

Arc-length formula.

Give arc length , a function of :

---

Compute .

Hyperbolic trig derivative:

---

Plug into formula.

Arc length:

---

Hyperbolic trig identity.

Fundamental identity:

Rearrange:

---

Plug into formula and compute.

Arc length:

Compute integral:

The arc length of a catenary curve matches the area under the catenary curve!

13 - Arc length, line segment

Find the arc length of the straight line given by the formula over .

Check your answer using the Pythagorean Theorem.

14 - Surface area of a sphere

Using the fact that a sphere is given by revolving a semicircle, verify the formula for the surface area of a sphere.

Solution Sphere as surface of revolution.

Sphere of radius given by revolving upper semicircle.

Upper semicircle:

Upper semicircle as function of :

---

Surface area formula.

Bounds are and .

Function is

Plug data into formula:

---

Compute .

Power rule and chain rule:

Algebra:

Squaring:

---

Compute integrand.

Compute :

Integrand factors become:

---

Compute integral.

Surface area again:

This is the desired surface area formula .