Stepwise problems - Thu. 11:59pm
Arc length
01
Arc length - reversed
and roles Find the arc length of the curve that satisfies the equation
over .
Surface areas of revolutions - thin bands
02
Surface area: revolved cubic
The curve
over is revolved around the -axis. Find the area of the resulting surface.
Regular problems - Sat. 11:59pm
Arc length
03
Arc length - tricky algebra
Find the arc length of the curve
for . (Hint: expand under the root, then simplify, then factor; now it’s a square and the root disappears.)
04
Arc length - tricky integration
Find the arc length of the curve
for . (Hint: the integral can be done using either: (i)
-sub then trig sub, or (ii) ‘rationalization’ then partial fractions.)
Surface areas of revolutions - thin bands
05
Surface area: cone
A cone may be described as the surface of revolution of a ray emanating from the origin, revolved around the
-axis. Let
for some . Find the surface area of the cone given by revolving the graph of around the -axis over . Can you also calculate this area using geometry? And verify the two methods give the same formula? (Hint: ‘unroll’ the cone into a sector.)
06
Surface area: parabolic reflector
A parabolic reflector is given by rotating the curve
around the -axis for . What is the surface area of this reflector?
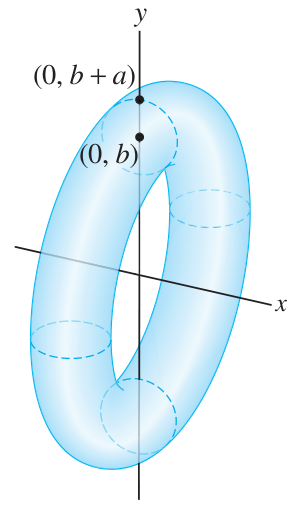
07
Surface area: torus
A torus is created by revolving about the
-axis the circle with this equation: Find the surface area of this torus.
(Hint: compute for the top and bottom of the circle separately and add the results.)