Stepwise problems - Thu. 11:59pm
Work performed
01
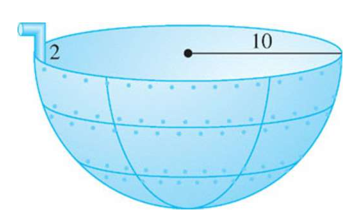
Pumping water from hemispherical tank
A hemispherical tank (radius
) is full of water. A pipe allows water to be pumped out, but requires pumping up above the top of the tank.
- (a) Set up an integral that computes the total work required to pump all the water out of the tank, assuming it is completely full.
- (b) Now assume the tank start out full just to
. What does the integral become?
02
Building a conical tower
Set up an integral that computes the work done (against gravity) to build a circular cone-shaped tower of height
and base radius out of a material with mass density .
Improper integrals
03
Comparison test
Use the comparison test to determine whether the integral converges:
Regular problems - Sat. 11:59pm
Work performed
04
Work to raise a leaky bucket
A bucket of water is raised by a chain to the top of a
-foot building. The water is leaking out, and the chain is getting lighter. The bucket weighs
, the initial water weighs , and the chain weighs , and the water is leaking at a rate of as the bucket is lifted at a rate of . What is the total work required to raise the bucket of water?
05
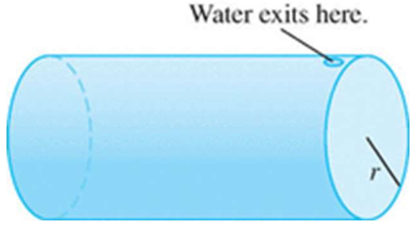
Work to pump water from cylindrical tank
A cylindrical tank is full of water and the water is pumped out the top. (See figure.) The length of the tank is
and the radius is .
- (a) Set up an integral for the total work performed assuming the tank is initially completely full.
- (b) Set up an integral for the total work performed assuming the tank is initially full to
and the water is pumped out of a spigot extending above the top of the tank.
06
Work to build a pyramid
The Great Pyramid of Giza is
tall and has a square base with on each side. It is built of stone with mass density . Set up an integral that computes the work (against gravity) required to build the pyramid.
Improper integrals
07
Proper vs. improper
For each integral below, determine whether it is proper or improper, and if improper, explain why.
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
08
Gabriel’s Horn - Volume and surface of revolution
The curve
for is rotated about the -axis. The resulting shape is Gabriel’s Horn.
- (a) Find the volume enclosed by the horn by evaluating a convergent improper integral.
- (b) Show that the surface area of the horn is infinite by applying comparison to a
-integral which is divergent.
09
Computing improper integrals, Part I
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
- (a)
- (b)
- (c)
10
Computing improper integrals, Part II
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
- (a)
- (b)
- (c)