Stepwise problems - Fri. 11:59pm
Sequences
01
L’Hopital practice - converting indeterminate form
By imitating the technique in from the L’Hopital’s Rule example, find the limit of the sequence:
02
Squeeze theorem
Determine whether the sequence converges, and if it does find its limit:
(a)
(b) (Hint for (b): Verify that
by comparing the to another copy of .)
Series
03
General term of a series
Write this series in summation notation:
(Hint: Find a formula for the general term
.)
04
Geometric series
Compute the following summation values using the sum formula for geometric series.
(a)
(b) (c) (d)
Regular problems - Mon. 10:00am
Sequences
05
Computing a sequence by terms
Calculate the first four terms of each sequence from the given general term, starting at
: (a)
(b) (c) (d) (e) (f)
06
General term of a sequence
Find a formula for the general term (the
term) of each sequence: (a)
(b) (c)
07
Limits and convergence
For each sequence, either write the limit value (if it converges), or write ‘diverges’.
(a)
(b) (c) (d) (d)
(e) (f) (g) (h)
(i) (j) (k) (l)
(m) (n) (o) (p)
(q) (r) (s) (t)
Series
08
Repeating digits
Using the geometric series formula, find the fractional forms of these decimal numbers:
(a)
(b)
09
Series from its partial sums
Suppose we know that the partial sums
of a series are given by the formula .
- (a) Compute
. - (b) Find a formula for the general term
. - (c) Find the sum
.
10
Geometric series - partial sums and total sum
Consider the series:
- (a) Compute a formula for the
partial sum . (You may apply the known formula or derive it again in this case using the “shift method.”) - (b) By taking the limit of this formula as
, find the value of the series. - (c) Find the same value of the series by computing
and and plugging into .
11
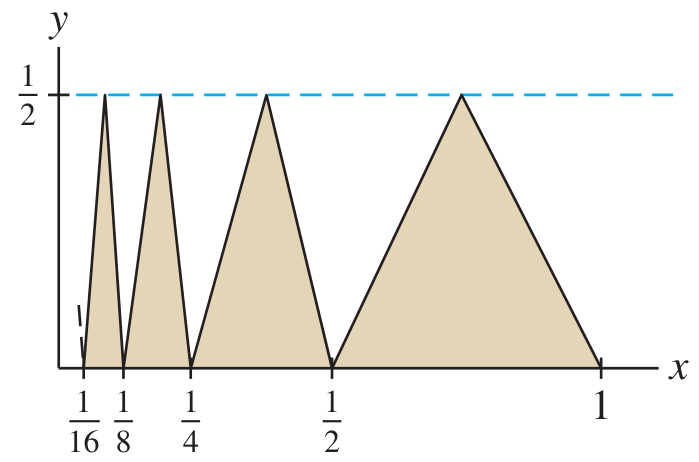
Total area of infinitely many triangles
Find the area of all the triangles as in the figure:
(The first triangle from the right starts at
, and going left they never end.)