Course Landing Page

W14 - HW Solutions

3 min read

04 - Arclength of one loop of a rose

Consider the graph of the polar curve .

Set up an integral which computes the arclength of one loop of this curve.

Solution

Find when for the bounds of the integral.

Set up integral.

07 - Sketching limaçons

Sketch the graphs of the following polar functions:

(a) ; (b) ; (c) ; (d)

Solution

(a) 200

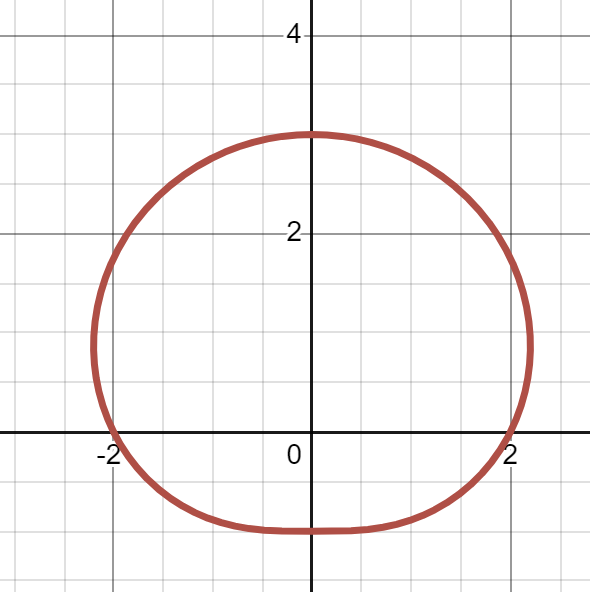
(b) 200

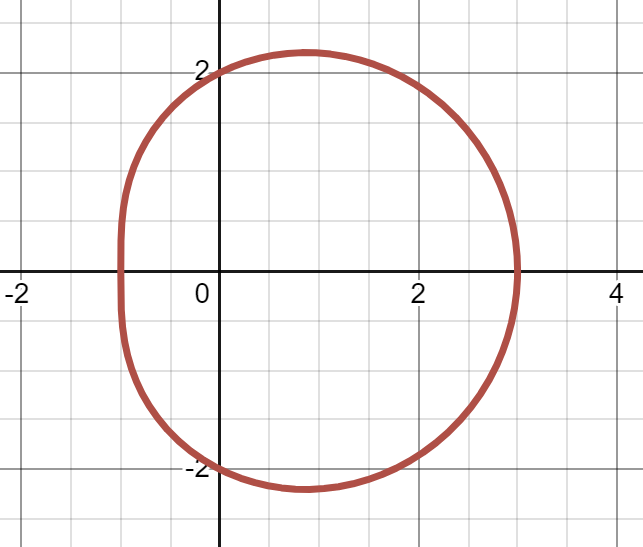
(c) 200

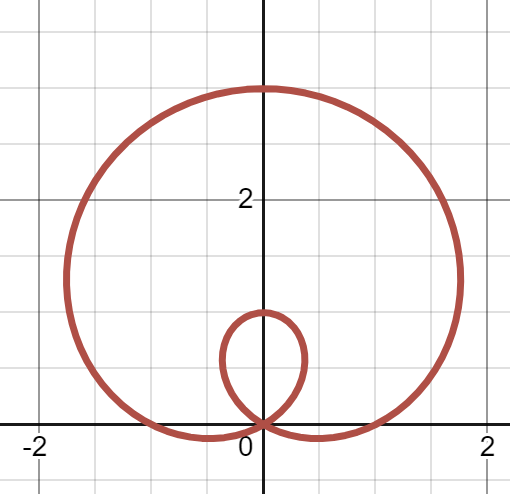
(d) 200

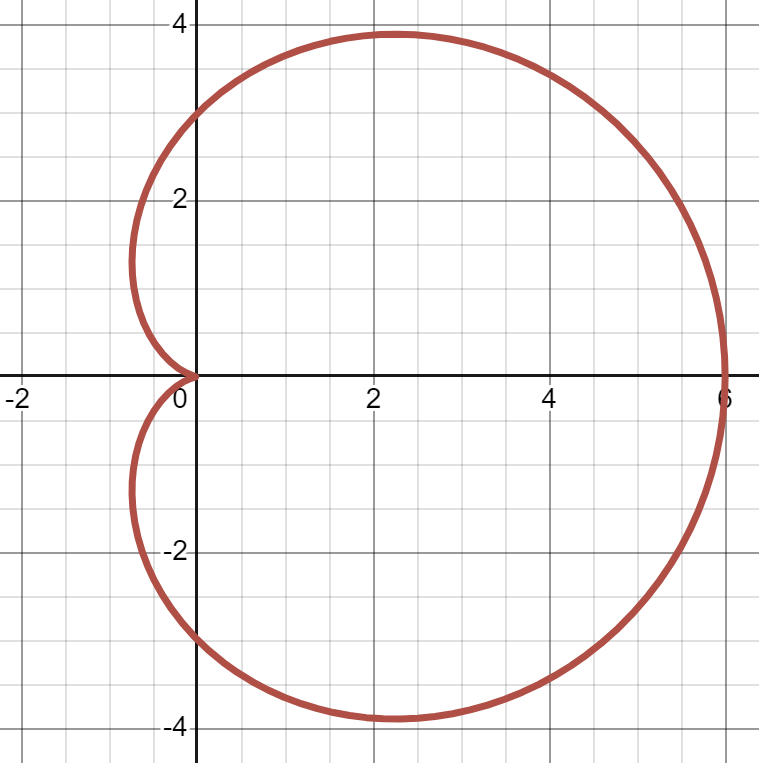
08 - Sketching roses

Sketch the graphs of the following polar functions. Use numbers to label the order in which the leaves/loops are traversed.

(a) ; (b) ; (c)

Solution

(a) 200

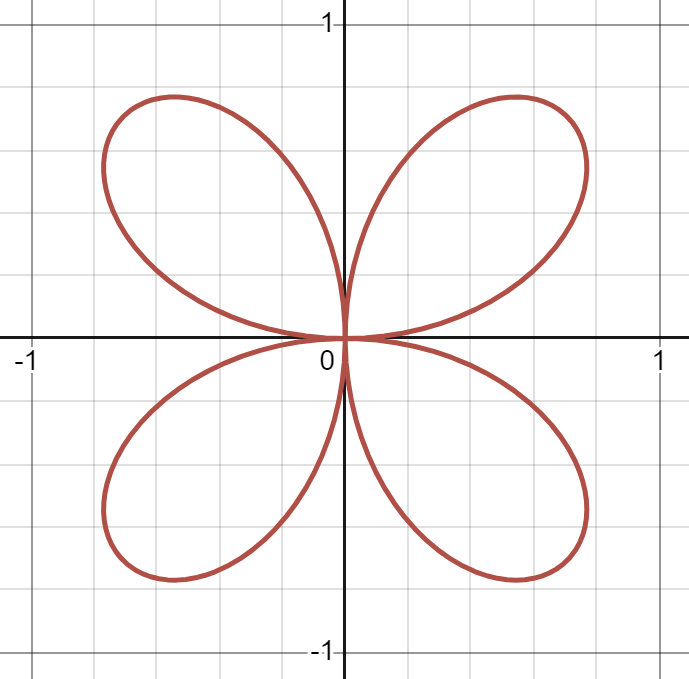
(b) 200

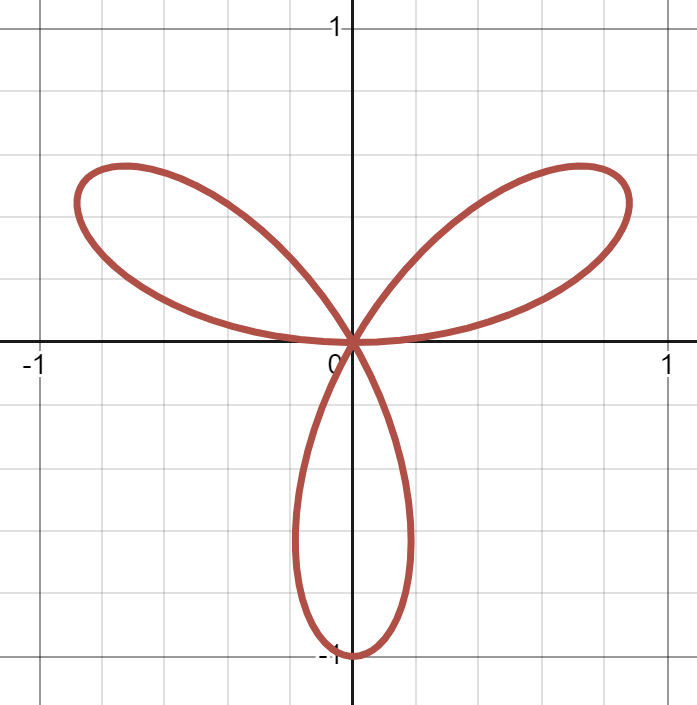
(c) 200

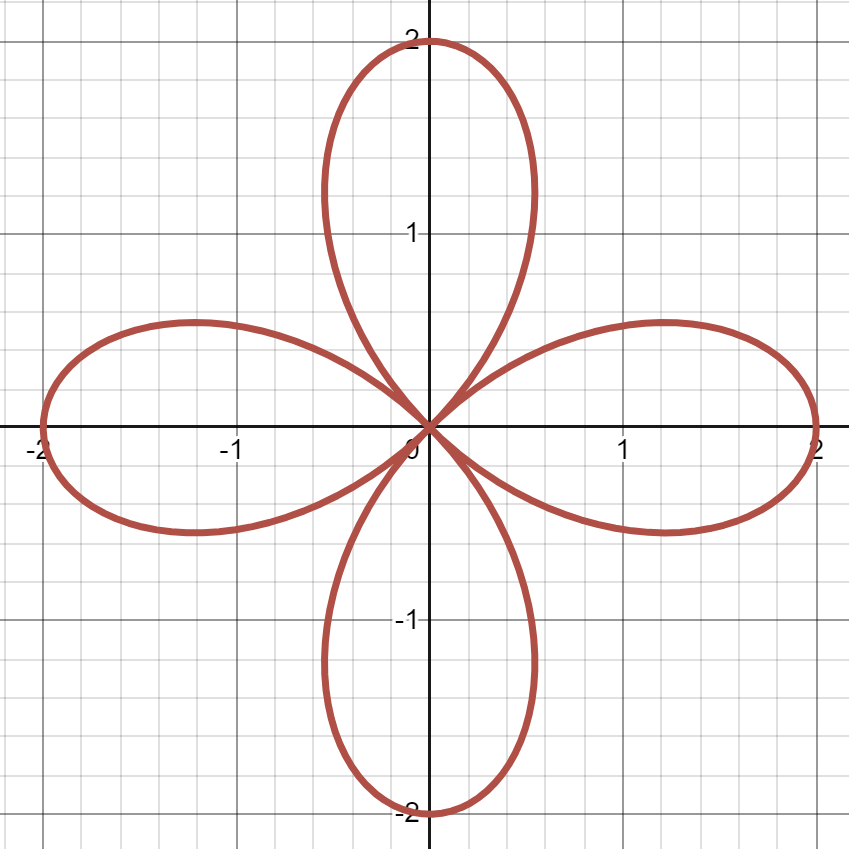
10 - Polar coordinates - lunar areas

(a) Find the area of the green region.

(b) Find the area of the yellow region.

Solution

(a)

Find the angle of the line of intersection between the two curves in the first quadrant.

Compute the area below the line of intersection and above the -axis.

Compute the area above the line of intersection and the upper half of the curve.

Add both areas and multiply by two (to account for the part in the fourth quadrant).

(b)

Compute the integral from the -axis to the line of intersection, subtracting the inner radius from the outer radius.

Multiply by two to account for the part in the fourth quadrant to find the total area.

11 - Pickup region of a microphone - limaçon area

The pickup region of a microphone is described by a limaçon with equation , and part of the region is on a stage.

Find the area of the part of the region on the stage.

Solution

Find the intersection between the line and the curve.

So, and .

Find the area.

12 - Area of an inner loop

A limaçon is given as the graph of the polar curve .

Find the area of the inner loop of this limaçon.

Solution

Find when to determine the bounds of our area integral.

Compute area.