Stepwise problems - Thu. 11:59pm
Polar curves
01
Convert points: Cartesian to Polar
Convert the Cartesian (rectangular) coordinates for these points into polar coordinates:
(a)
(b) (c) (d)
02
Convert equations: Polar to Cartesian
Convert the polar equation to a Cartesian equation. Be sure to simplify.
(a)
(b) (c)
Calculus with polar curves
03
Polar curve - Vertical or horizontal tangent lines
Find all points on the given curve where the tangent line is horizontal or vertical.
Hint: First determine parametric Cartesian coordinate functions using
as the parameter.
04
Arclength of one loop of a rose
Consider the graph of the polar curve
. Set up an integral which computes the arclength of one loop of this curve.
Regular problems - Sat. 11:59pm
Polar curves
05
Convert points: Polar to Cartesian
Convert the polar coordinates for these points into Cartesian (rectangular) coordinates:
(a)
(b) (c) (d)
06
Convert equations: Cartesian to Polar
Convert the Cartesian equation to a polar equation. Be sure to simplify.
(a)
(b) (c)
07
Sketching limaçons
Sketch the graphs of the following polar functions:
(a)
(b) (c)
(d)
08
Sketching roses
Sketch the graphs of the following polar functions. Use numbers to label the order in which the leaves/loops are traversed.
(a)
(b) (c)
Calculus with polar curves
09
Polar curve - Slope of tangent line
Find the slope of the tangent line to the given polar curve:
Hint: First determine parametric Cartesian coordinate functions using
as the parameter.
10
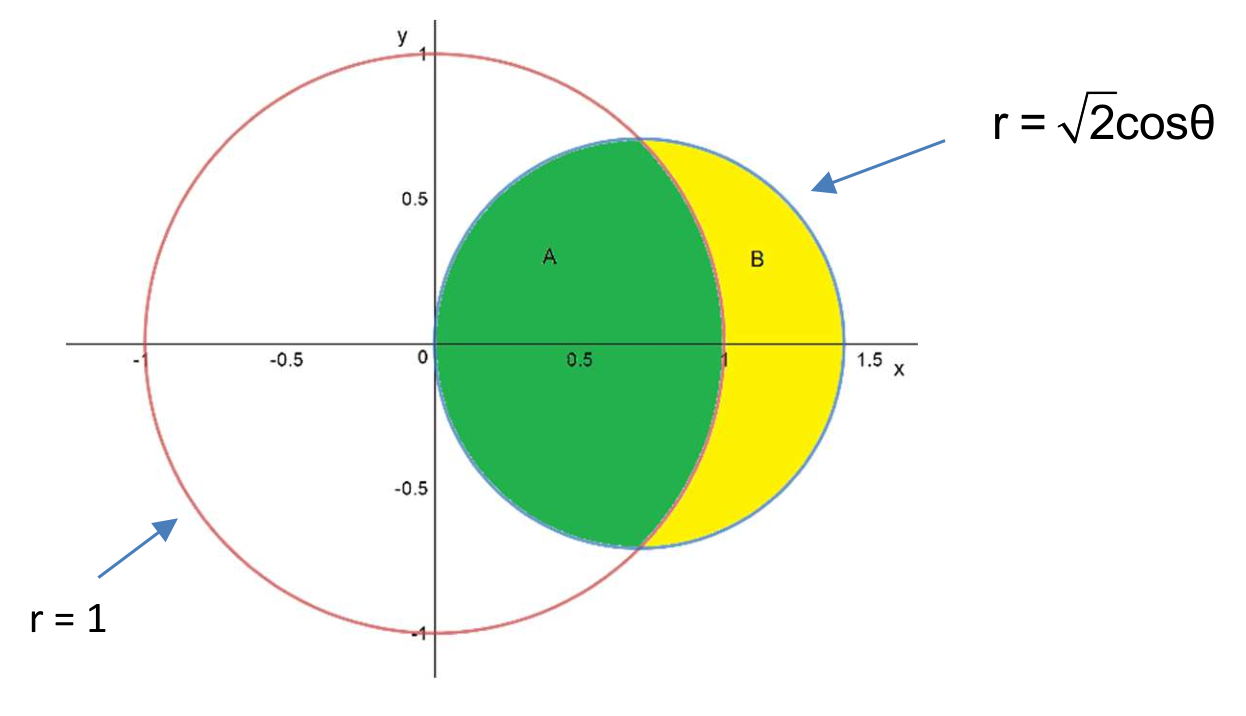
Polar coordinates - lunar areas
(a) Find the area of the green region.
(b) Find the area of the yellow region.
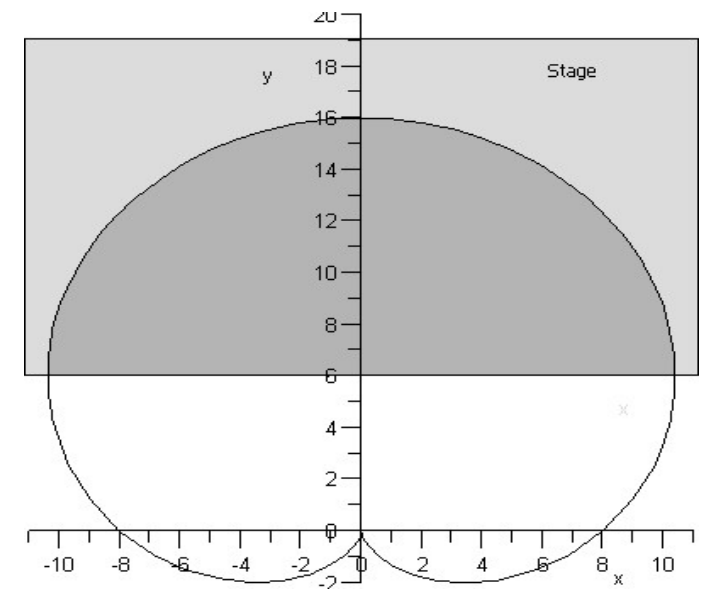
11
Pickup region of a microphone - limaçon area
The pickup region of a microphone is described by a limaçon with equation
, and part of the region is on a stage. Find the area of the part of the region on the stage.
12
Area of an inner loop
A limaçon is given as the graph of the polar curve
. Find the area of the inner loop of this limaçon.