Complex algebra
Videos, Organic Chemistry Tutor
01 Theory - Complex arithmetic
The complex numbers
To add, subtract, scale, and multiply complex numbers, treat ‘
Simplify the result using
For example:
Complex conjugate
Every complex number has a complex conjugate:
For example:
In general,
Conjugates are useful mainly because they eliminate imaginary parts:
In general:
Complex division
To divide complex numbers, use the conjugate to eliminate the imaginary part in the denominator.
For example, reciprocals:
More general fractions:
Multiplication preserves conjugation
For any
: Therefore, one can take products or conjugates in either order.
02 Illustration
Example - Complex multiplication
Complex multiplication
Compute the products:
(a)
(b) Solution
(a)
Expand:
Simplify
:
(b)
Expand:
Simplify
: Link to original
Example - Complex division
Complex division
Compute the following divisions of complex numbers:
(a)
(b) (c) (d) Solution
(a)
Conjugate is
: Simplify:
(b)
Conjugate is
:
(c)
Factor out the
: Use
:
(d)
Denominator conjugate is
: Simplify:
Link to original
Complex exponential
Videos, Khan Academy
03 Theory - cis, Euler, products, powers
Multiplication of complex numbers is much easier to understand when the numbers are written using polar form.
There is a shorthand ‘
The
For example:
Euler Formula
General Euler Formula:
On the unit circle:
The form
The principal advantage of the form
Complex multiplication - Exponential form
In words:
- Multiply radii
- Add angles
Notice:
Notice:
Therefore
De Moivre’s Theorem - Complex powers
In exponential notation:
In
notation: Expanded
notation:
So the power of
- Stretch:
- Rotate by
Extra - Derivation of Euler Formula
Recall the power series for
: Plug in
: Simplify terms:
Separate by
-factor. Select out the : Separate into a series without
and a series with : Identify
and . Write trig series: Therefore
.
04 Illustration
Example - Complex product, quotient, power using Euler
Complex product, quotient, power using Euler
Start with two complex numbers:
Product
: Quotient
:
Power
: Notice:
Simplify:
Thus:
Link to original.
Example - Complex power from Cartesian
Complex power from Cartesian
Compute
. Solution
First convert to exponential form:
Compute the power:
Link to original
Complex roots
Videos, Trefor Bazett
- Finding cube roots: Find cube roots of
Videos, Brain Gainz
- Finding nth roots: Fourth roots of
05 Theory - Roots formula
The exponential notation leads to a formula for a complex
Every complex number actually has
distinct complex roots! That’s two square roots, three cube roots, four
roots, etc.
All complex roots
The complex roots of
are given by: In Cartesian notation:
In words:
- Start with the basic root:
- Rotate by increments of
to get all other roots
Extra - Complex roots proof
We must verify that
:
06 Illustration
Example - Finding all
roots of Finding all 4th roots of 16
Compute all the
roots of . Solution
Write
. Evaluate roots formula:
Simplify:
Link to original
Example - Finding
roots of Finding 2nd roots of 2i
Find both
roots of . Solution
Write
. Evaluate roots formula: Compute the options:
: Convert to rectangular:
Link to original
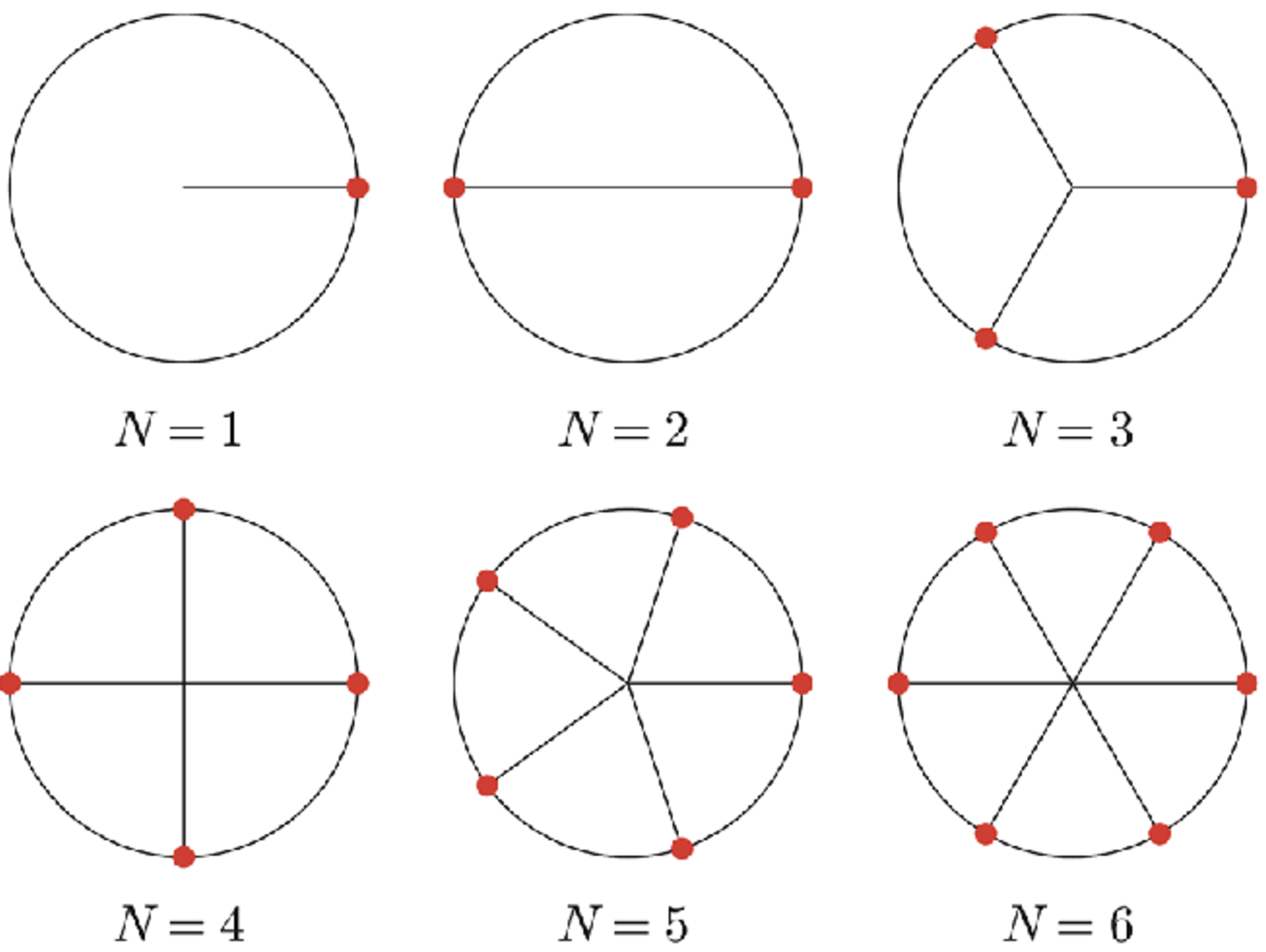
Example - Some roots of unity
Some roots of unity
Find the
and and and and and roots of the number . Solution
Write
. Evaluate roots formula. There is no possible :
Write
. Evaluate roots formula in terms of : Compute the two options,
:
Evaluate roots formula in terms of
: Compute the options:
:
Evaluate roots formula:
Compute the options:
:
Evaluate roots formula: Compute the options:
: Don’t simplify, it’s not feasible.
Evaluate roots formula:
Compute the options:
: Simplify:
Link to original