Stepwise problems - Thu. 11:59pm
Shells
01
01
Shells volume - offset graph,
-axis Consider the region in the first quadrant bounded by the lines
, , , and the curve . Revolve this about the -axis. Find the volume of the resulting solid.
Link to originalSolution
01
(1) Set up integral.
(2) Perform
-substitution with and :
(3) Integrate with power rule:
Link to original
IBP
02
01
Integration by parts - A and E
Compute the integral:
Solution
02
(1) Select
and considering LIATE:
(2) Apply IBP formula
:
Note A: We can change notation
Link to originalto because the value of is arbitrary.
03
02
Integration by parts - A and T
Compute the integral:
Solution
03
(1) Select
and considering LIATE:
(2) Apply IBP formula
:
(3) Select another
and and do IBP again:
(4) Put all together in (A):
Note B: We can change notation
Link to originalto because the value of is arbitrary.
Regular problems - Sun. 11:59pm
Shells
04
02
Shells volume - set up integrals, both axes
Consider the region in the first quadrant bounded by the lines
and , and the curve . Set up integrals to find the volumes of the solids obtained by revolving this region about (i) the
-axis, and (ii) the -axis. (No need to evaluate these integrals.) Solution
04
You can set up each integral using disks/washers or using shells.
(i) Using washers, obtain:
Using shells, obtain:
(ii) Using disks, obtain:
Using shells, obtain:
Link to original
05
03
Shells volume - shells v. washers
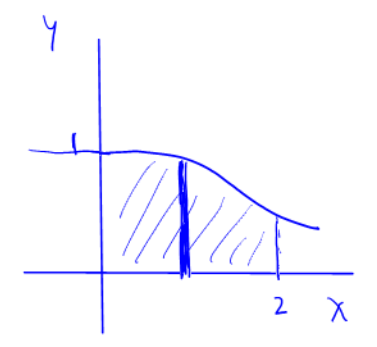
Consider the region in the
-plane, in the first quadrant, bounded by the -axis on the left, by on the top, and on the bottom.
A 3D solid is given by revolving this region around the
-axis.
- (a) Find the volume of the solid using the method of shells.
- (b) Attempt to find the volume of the solid using the method of washers/disks. Why is this harder? (TWO reasons!)
Link to originalSolution
05
(a)
(1) Write down shells formula:
(2) Define the cross section region:
Bounded above by
. Bounded below by . Bounded left by
. Bounded right by intersection at line .
(3) Define
and and :
(4) Plug into shells formula and compute:
(b)
(1) Write down washers formula using
:
(2) Rewrite bounding equations in terms of
:
(3) Determine region boundary data:
Bounded above by
. Bounded below by . Intersection at .
(4) Determine
in two components, with the dividing line: Note that
for both regions. These are disks.
(5) Compute the integral:
(6) Why are shells preferable?
Link to original
- Only need one integral.
- Don’t need to rewrite boundary equations in terms of
.
IBP
06
03
Integration by parts - A and L
Compute the integral:
Solution
06
(1) Select
and considering LIATE:
(2) Apply IBP formula
: Link to original
07
04
Integration by parts - A and E
Compute the integral:
Solution
07
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral: Link to original
08
05
Integration by parts - A and I
Compute the integral:
Solution
08
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral:
(3) Perform
-sub with and :
(4) Insert result in Exp. (A):
Note B: We can change
Link to originalto because the inner expression is never negative.
09
06
Integration by parts - E and T, ‘breaking the circle’
Compute the integral:
You should perform IBP twice, find an equation, and use algebra to solve it (‘breaking the circle’) for the desired integral.
Link to originalSolution
09
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral: Therefore:
(3) Repeat. Select
and considering LIATE:
(4) Apply IBP formula
and compute integral:
(5) Now insert in Eqn. A:
Introduce notational label:
Now use this label in Eqn. A and solve for
: Link to original