W02 - HW Solutions

01

(1) Notice odd power on . Swap the even bunch:

---

(2) Integrate with -sub setting and thus :

02

(1) Notice . Therefore integrate with -sub setting and :

03

(1) Notice all even powers. Use power-to-frequency conversion:

Plug in:

Simplify:

---

(2) Reduce power again for :

(This is derived from the power-to-frequency formula by changing ‘’ to ‘’ in that formula.)

---

(3) On the last term, swap even bunch:

Plug all in and obtain:

---

(4) Integrate the first three terms:

---

(5) Integrate the last term with -sub, setting and :

---

(6) Combine in final result:

Note: It is also possible to rewrite using trig identities. So, equally valid answers may look different than this.

04

(1) Substitute and thus . Adjust the bounds as follows:

Rewrite the integral:

---

(2) Use power-to-frequency conversion:

---

Note A: Use , then and this equals for .

05

(1) Trig substitution. Notice , so we should make use of the identity .

Pick and thus .

Then:

Plug in:

(We assume that for the relevant values of .)

---

(2) Perform integration.

Either recall from memory, or multiply above and below by , and obtain:

---

(3) To convert to we need given that .

Draw triangle expressing :

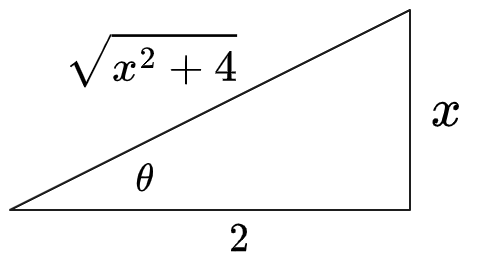
Therefore . We already know . Thus:

---

(4) Simplify with log rules:

06

(1) Notice odd power on . Swap the even bunch:

---

(2) Perform -sub setting and thus :

---

(3) Convert back to :

07

(a) Select and thus :

---

(b)

(1) Select and thus :

---

(3) Swap even bunch using :

---

(4) Perform -sub with and integrate:

08

(1) Change variable by substituting and :

---

(2) Identify :

---

(3) Perform -sub with and thus :

09

(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Plug in and simplify:

(We must assume that for the relevant values of here.)

---

(2) Use power-to-frequency conversion:

---

(3) Convert back to terms of :

First draw a triangle expressing :

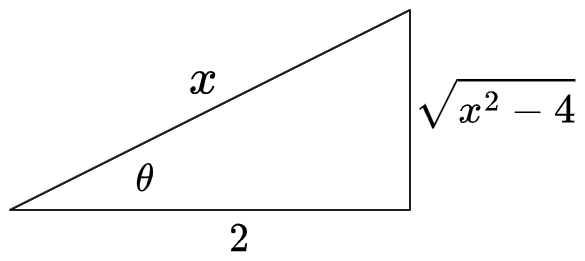
Therefore:

For , use the double-angle identity:

Therefore:

10

(1) Complete the square:

---

(2) Substitute and thus :

---

(3) Convert back to terms of :

First draw a triangle expressing :

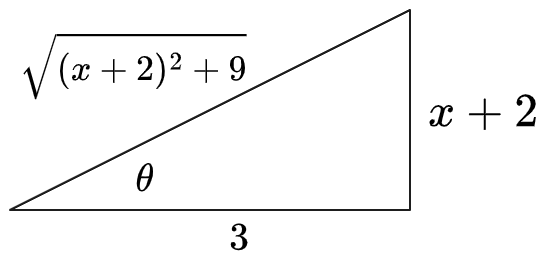
It follows that . Then:

---

Note A: Using log rules, the denominator can be brought out as which can be “absorbed” into the constant .

11

(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

---

(2) Convert to and integrate:

---

(3) Convert back to terms of :

Draw a triangle expressing :

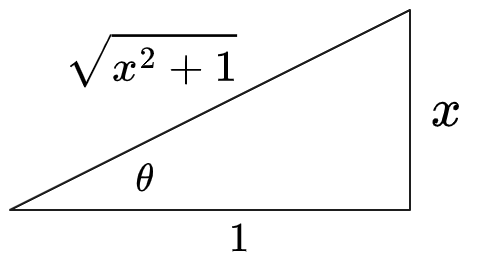
Therefore and . Then:

12

(1) Perform -sub setting and thus . Adjust the bounds as follows:

Therefore:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Adjust bounds:

Therefore:

---

(3) Integrate from memory or multiplying above and below by :

13

(1) Take out constants and insert given values:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Adjust bounds:

Then:

---

(3) Integrate:

---

(4) Compute :

Draw a triangle expressing :

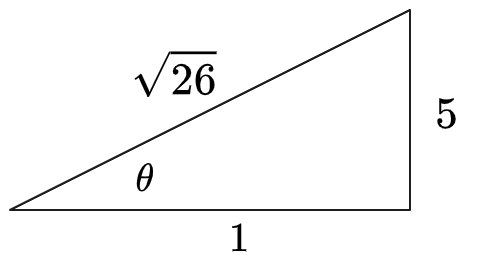
Therefore . Then: