Differential Equations - Packet 05

Applications: qualitative behavior

Paths in the plane

A classical set of applications of first-order ODEs involves finding paths through space with specific properties.

Example

Catenary

Problem: A catenary is the shape formed by a hanging chain, string, or cable, and also the shape formed by a stable arch. A cable can only resist expansion forces directed along its length, while an arch can only resist compression forces directed along its length. What is the shape of a catenary?

Solution: Consider a hanging chain. Let be the tension force tangent to the chain at a point , and let be the horizontal component of the tension, so , where is the angle formed by the line tangent to the chain at .

The vertical balance of forces is more complicated. Set at the lowest point on the chain, and let measure the arclength of the chain with . At , the chain has a horizontal slope, so the vertical component of tension force there is zero. At , the vertical component of tension force is . The total vertical force on the portion of chain from the bottom up to is therefore , and this must balance the total weight of the chain from the bottom up to , which is , where is the chain density. So .

By dividing our two equations, we have . We may write for the slope of the tangent at . This gives us the differential equation . To solve this, we need to relate the arclength function to . Recall the arclength formula:

Plugging this in gives a differential equation that can be solved algebraically. The solution (family of curves) is:

If we set , i.e. the vertical position of the bottom of the chain, we can solve for and obtain:

https://www.desmos.com/calculator/ngjjfg5yxj

Question 05-01

Solve the ODE

Solve (algebraically) the ODE used to define the catenary curve. (Hint: differentiate the function , substitute in, then use a reduction of order.)

Question 05-02

Arch vs. chain

Why does the St. Louis arch (or any other self-supporting arch) also have a catenary shape?

Example

Tractrix

A tractrix is a curve given by dragging a point behind a string of fixed length.

Problem: Suppose we drag the point behind a string of length . Suppose starts at , and we start at and walk in the direction. What is the shape of the path of ?

Solution: Write . The tangent line to the string at has slope given by

To see this, draw the triangle with vertices and and . The hypotenuse of this triangle is the string itself, and we are pulling from the top vertex.

This equation is separable, and the solution is:

https://www.desmos.com/calculator/9mu1stojhl

Question 05-03

Pushing a pole

Suppose a pole is pushed from one end, with a free pivot on the end from which it is pushed. The shape of the path taken by the opposite end is also a tractrix. Why?

(Describe the concept of tractrix in such a way that it applies equally to dragging strings and pushing poles.)

Catenary vs. tractrix The catenary curve is the evolute of the tractrix; the tractrix is the involute of the catenary. https://en.wikipedia.org/wiki/Involute#Involute_and_evolute

Example

Pursuit curve

Problem: A gazelle runs up the -axis at speed starting at , and a cheetah runs towards the gazelle at speed starting at . What is the shape of the path taken by the cheetah?

Solution: The gazelle’s path can be given parametrically by the curve . Suppose the cheetah is at point . The vertical distance from cheetah to gazelle is , and the horizontal distance is .

We assume the cheetah is always running straight toward the gazelle, so the slope of the tangent line to the cheetah’s path is , and we obtain the differential equation:

This equation involves two independent variables, and , so we cannot immediately solve it. Of course they are related by the fact that is the -coordinate of the cheetah’s path. We would like to eliminate from the equation by substituting a formula for in terms of , , and quantities. This is the hard part.

We know that the cheetah is running at speed , so we also have the equation:

(Here we use for the arclength of the cheetah’s path.) This equation relates to the quantities , , and .

Now we seek to combine the equations. We can flip the second equation to obtain

If we differentiate the first equation in , we can make the disappear, with appearing instead:

Set . Reduce the order using and obtain:

Integrate this again to find , solving for the constant using the initial condition :

https://www.desmos.com/calculator/geosk6qjrb

Question 05-04

Checking algebra

Check the algebra for the solution of and then the integration for . (Write out all intermediate steps.)

Growth and decay

Another classic application of differential equations produces exponential growth and decay. Variants on this theme can account for recurring additions and subtractions.

Example

Growth of retirement fund with compound interest

A quantity of money in a savings account with compound interest rate grows according to the differential equation . The solution of this equation is an exponential function , where is the initial quantity in the account.

Theory: Compound interest with continuous deposit or withdrawal Suppose you make continuous deposits or withdrawals at a rate of (in dollars per year, with for deposits, for withdrawals). Now the equation is:

This equation is linear and separable. The solution can be found algebraically:

If the account starts with , then and .

Achieving a retirement fund Suppose this situation describes your Roth IRA. How much should you deposit in the account per year to achieve $800,000 after 40 years, with ? Answer:

Constant rate of retirement withdrawal, with inflation Suppose you have a retirement account with dollars, growing at the interest rate , and you plan to withdraw money at a rate which is increasing with inflation at per year, and starting at $80,000 per year. What should be to ensure you will have money for 30 years of retirement?

This problem involves two exponential growths, one stemming from interest and the other from inflation. The rate of withdrawal satisfies , so per year. Then the account value satisfies:

This equation is linear. The solution is:

Setting , we can solve for . Then plugging in , obtain the equation:

Setting 80,000r=0.05k=0.02A_01,580,000.

Exercise 05A-01

Design your traditional IRA

You are planning a traditional IRA for retirement: contributions during your working life are pre-tax, and withdrawals during retirement are taxed according to your income bracket when withdrawing. Your plan is to start the fund with $20,000 when you turn 30, and then to contribute a fixed yearly amount (modeled with a continuous yearly addition rate) each year until you turn 65. You invest the IRA in a broad market index with average yearly returns of 10% (not adjusted for inflation). Starting at age 65 you stop contributing and start withdrawing $70,000 per year after taxes for the next 25 years of retirement, and you would like to have $200,000 remaining in your estate at age 90, both figures measured in today’s dollars. Your tax bracket with this retirement income is 20%. Inflation is assumed to be a steady 2.5% per year. Everything is compounded continuously. What should you choose for the yearly contributions ?

Example

RC Circuits

An electrical circuit with a single resistor and a single capacitor is called an RC circuit: Suppose the voltage source produces a voltage between its terminals, and write and for the voltage drops across the resistor and capacitor.

By Ohm’s Law, , where is the current flowing through the resistor, and is the resistance of the resistor (a constant). The capacitor voltage drop satisfies , where is the charge stored in the capacitor, and is the capacitance of the capacitor (a constant). Current is the rate of flow of charge per unit time: .

By Kerchoff’s Voltage Law, we have an equation for the circuit:

So we find that charge satisfies:

which is a linear ODE. Solving this ODE and dividing by gives us a formula for :

Let us study this solution. The first term, , represents exponential decay from to . The second term depends on the source function . For example, if a constant, then the entire second term reduces to itself, and the solution will exponentially decay from down to .

Here is a Mathlet that shows the response when the source is a rectangular wave: https://mathlets.org/mathlets/periodic-box/

Exercise 05A-02

Bacteria growth on surface of spherical clump

A spherical clump of bacteria is growing in such a way that only the bacteria on its surface can reproduce, because only these are exposed to new food sources in the environment, while these surface bacteria do reproduce with exponential growth. Recall the formulas for volume and surface area of a sphere:

Find a differential equation satisfied by the number of bacteria as a function of time.

Autonomous equations

In a first calculus class, the sign of the derivative of a function is written on the number line in order to indicate places where is increasing or decreasing. This technique is useful for determining whether a critical point is a local min, max, or neither.

The same technique is used to study first-order autonomous differential equations. Autonomous equations having the form , meaning that the defining function does not involve the independent variable .

The main differences are: (i) for autonomous ODEs we have the derivative but we do not already have the function , and (ii) for autonomous ODEs we draw the signs of as vertical arrows (up or down) on a vertical line, instead of “” and “” on a horizontal line. We can add filled dots where , and open dots or dashed lines where , since these lines have special meaning.

This vertical number line we use to analyze is called a phase line. Phase lines can be used to make qualitative observations about the behavior of solutions to autonomous ODEs.

Lines corresponding to zeros of yield flat solutions. If the derivative is negative at such a line, i.e. , so cross through zero from above to below, then solutions will be attracted to the line . These lines are called stable equilibria. If then solutions will be repelled from the line. These lines are called unstable equilibria. (Sometimes stable equilibria are called sinks and unstable ones which are repulsive on both sides are called sources, while unstable ones that are repulsive on one side and attractive on the other side are called nodes.)

When , the equilibrium could be stable, unstable, or neither, and additional information is needed. The situation is the same as for critical points of a function that fails the second-derivative test.

Phase lines:

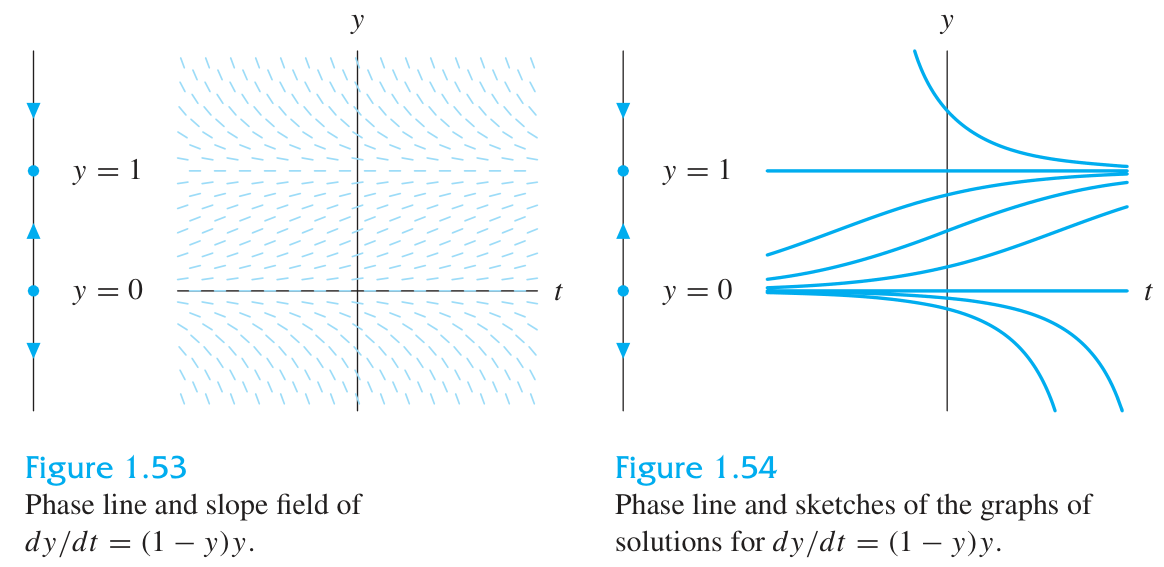
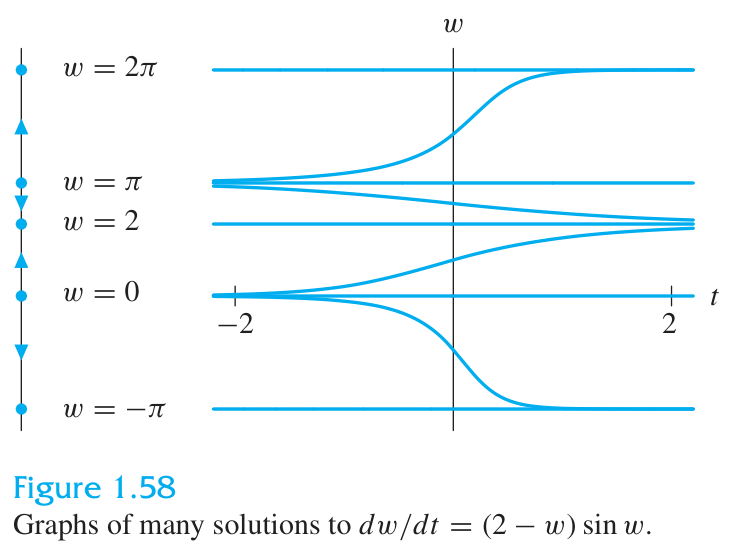
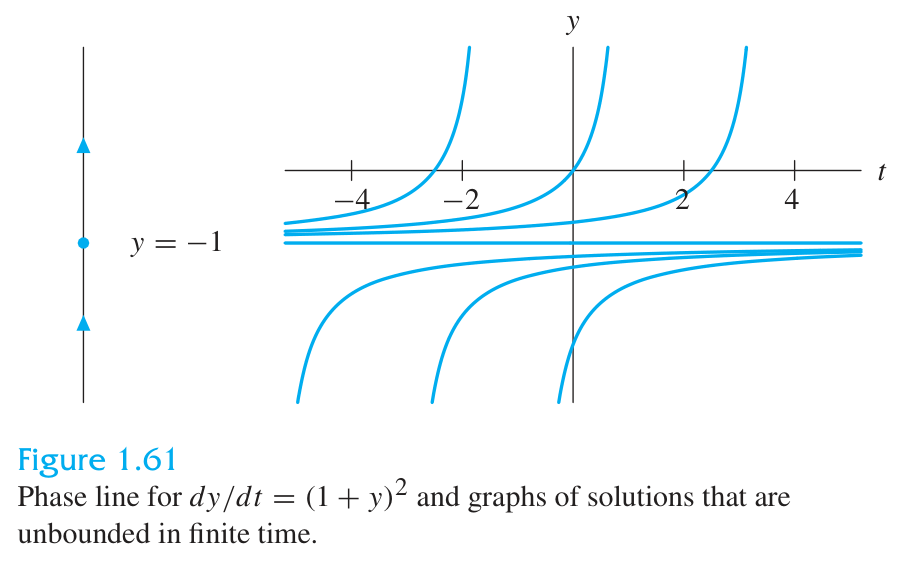
Phase lines with 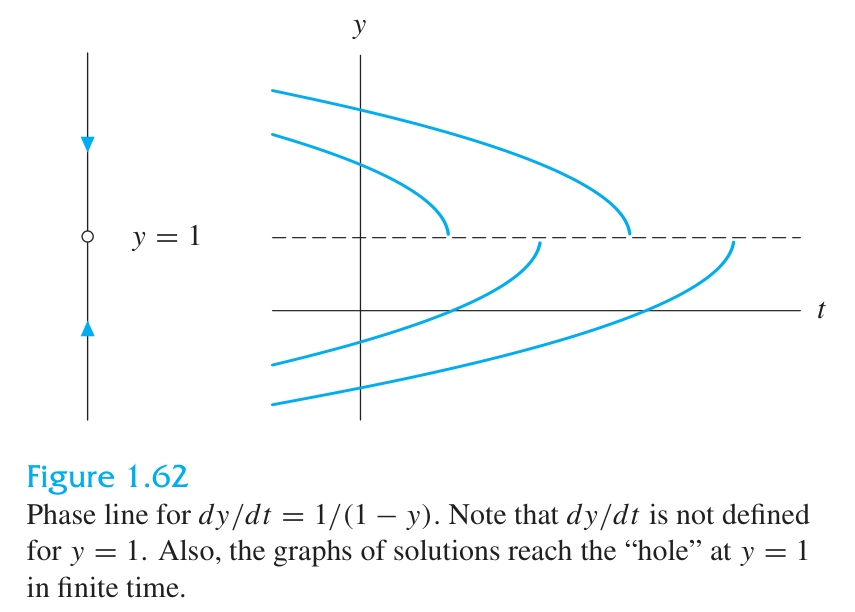at :

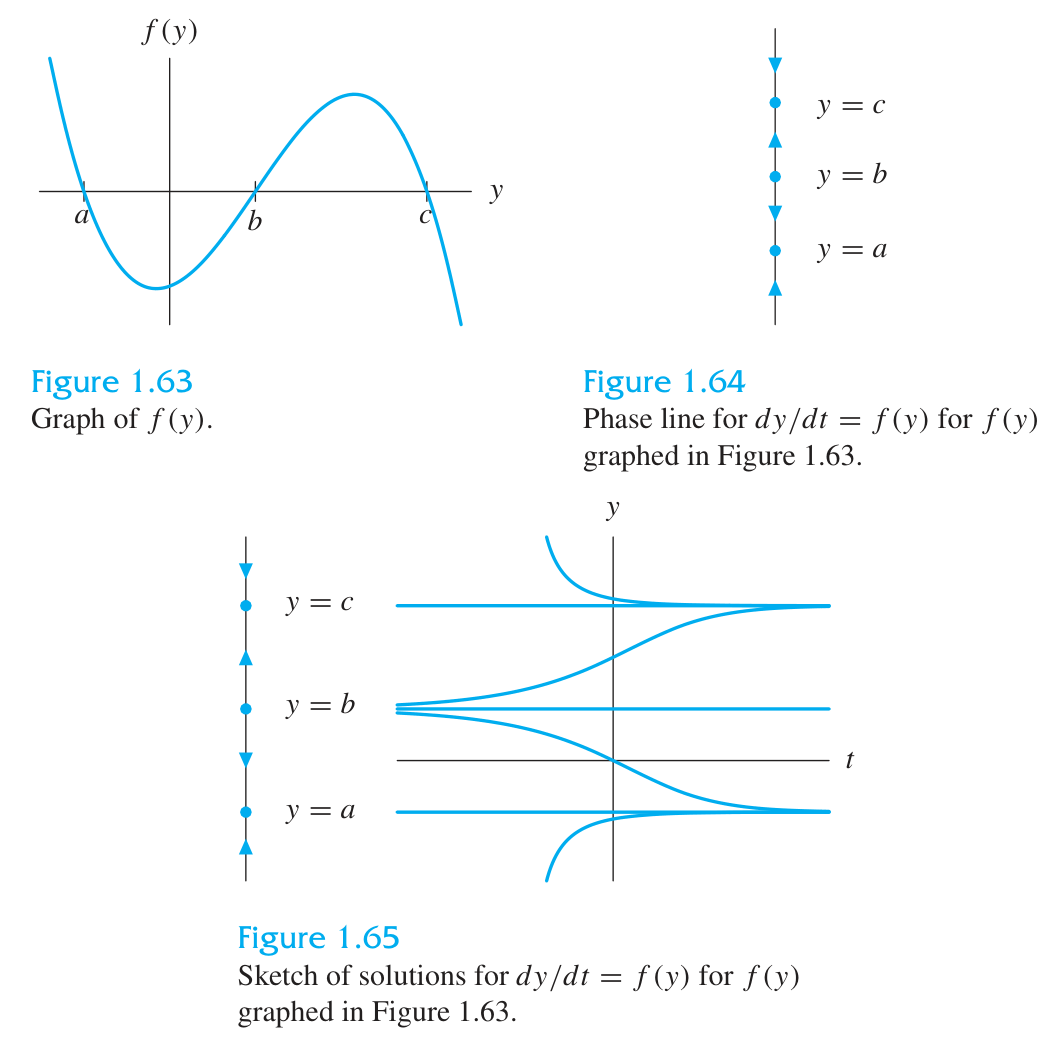
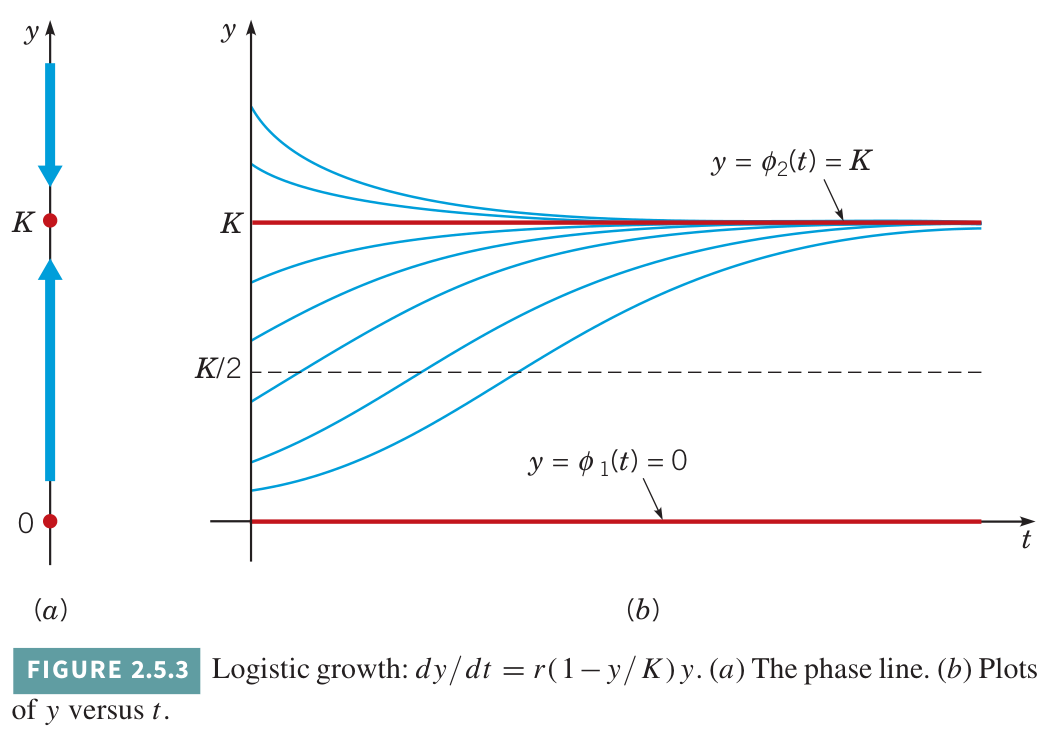
Phase lines deduced from the graph of alone:

Logistic growth Many natural systems experience exponential growth and decay only to first order. Once the exponential behavior has occurred for significant time, environmental effects of the growth or decay begin to modulate the rate of that growth or decay.

Exponential growth satisfies the equation , where is a constant giving the growth rate. We can modify the equation to account for changes of growth rate that depend on the quantity by letting become a function .

Example

Logistic curve: population dynamics

Modified exponential growth with a growth rate given by the linear function gives the logistic equation:

Using the theory of phase lines, we can study solutions to this equation without finding an explicit formula for them. Write , so . This number is sometimes called the carrying capacity of the population’s environment, because the growth rate will go negative when exceeds .

Now let us classify equilibrium points. We have . Compute

so and . Therefore is an unstable equilibrium, while is a stable equilibrium.

The logistic equation is separable, and it can be solved exactly and explicitly. Solutions are called logistic curves. These are given by:

Consider the interpretation of this formula. The initial value is . As , the second term in the denominator goes to zero. So as . This is true whether or .

It is useful to observe that the concavity of the solution trajectories can be ascertained from the formula for without actually solving the logistic equation. This relies on the chain rule:

For the logistic equation we are considering, this product is:

The inflection point is where this function changes sign, which is at , so the rate of population increase starts slowing down when the population is halfway to the carrying capacity of the environment.

Exercise 05B-01

Studying an autonomous equation

Sketch the phase line of the following ODE:

Classify each equilibrium trajectory as stable or unstable. Draw some representative solution trajectories using the qualitative information of your phase line.

Exercise 05B-02

Gompertz equation

Tumor growth is sometimes modeled by the Gompertz equation:

What are the equilibrium lines? Are they stable or unstable? What is the inflection point on a trajectory from the lower to the upper equilibrium?

Now solve the equation explicitly.

Problems due Monday 19 Feb 2024 by 1:00pm

Problem 05-01

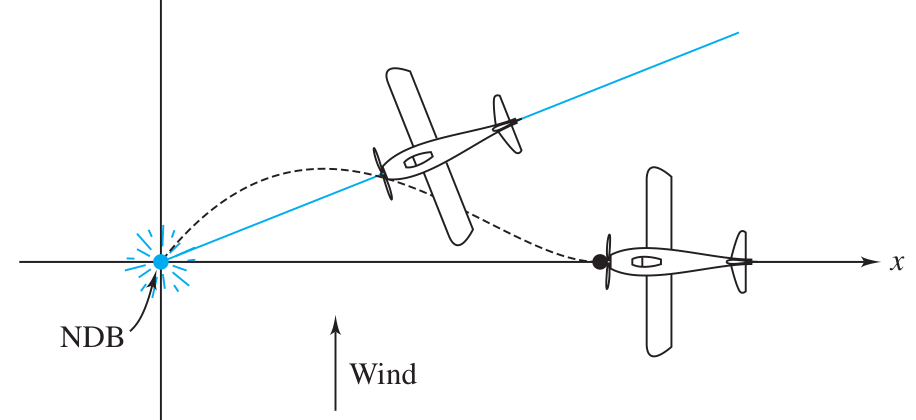
Pursuit with a crosswind

An airplane starts at and flies to the origin , but there is a crosswind. The wind blows in the direction at a constant speed , and the airplane flies with a fixed speed relative to the air around it. The plane always flies with its fuselage pointing towards . Assume . Find the path taken by the plane over the ground. (Hint: recall that .)

Problem 05-02

Escape velocity

A body is launched towards space from the surface of the earth. Assume the force of gravity on the body is given by , where is the radius of the earth, is the altitude of the body above the surface of the earth, and and are constants representing the mass of the body and the gravitational constant. Ignore air resistance. What is the minimum launch velocity needed for the body to escape earth’s gravity?

• Using Newton’s Law, write down a differential equation satisfied by the body during flight.
• Write this equation in terms of the velocity (dependent) and altitude (independent). (You will need to eliminate using the chain rule.)
• Solve this equation by separating variables, writing an explicit function . Use the initial condition .
• Find the maximum altitude in terms of . (Find when .) Now find which produces an infinite maximum altitude.

Problem 05-03

Coffee cooling

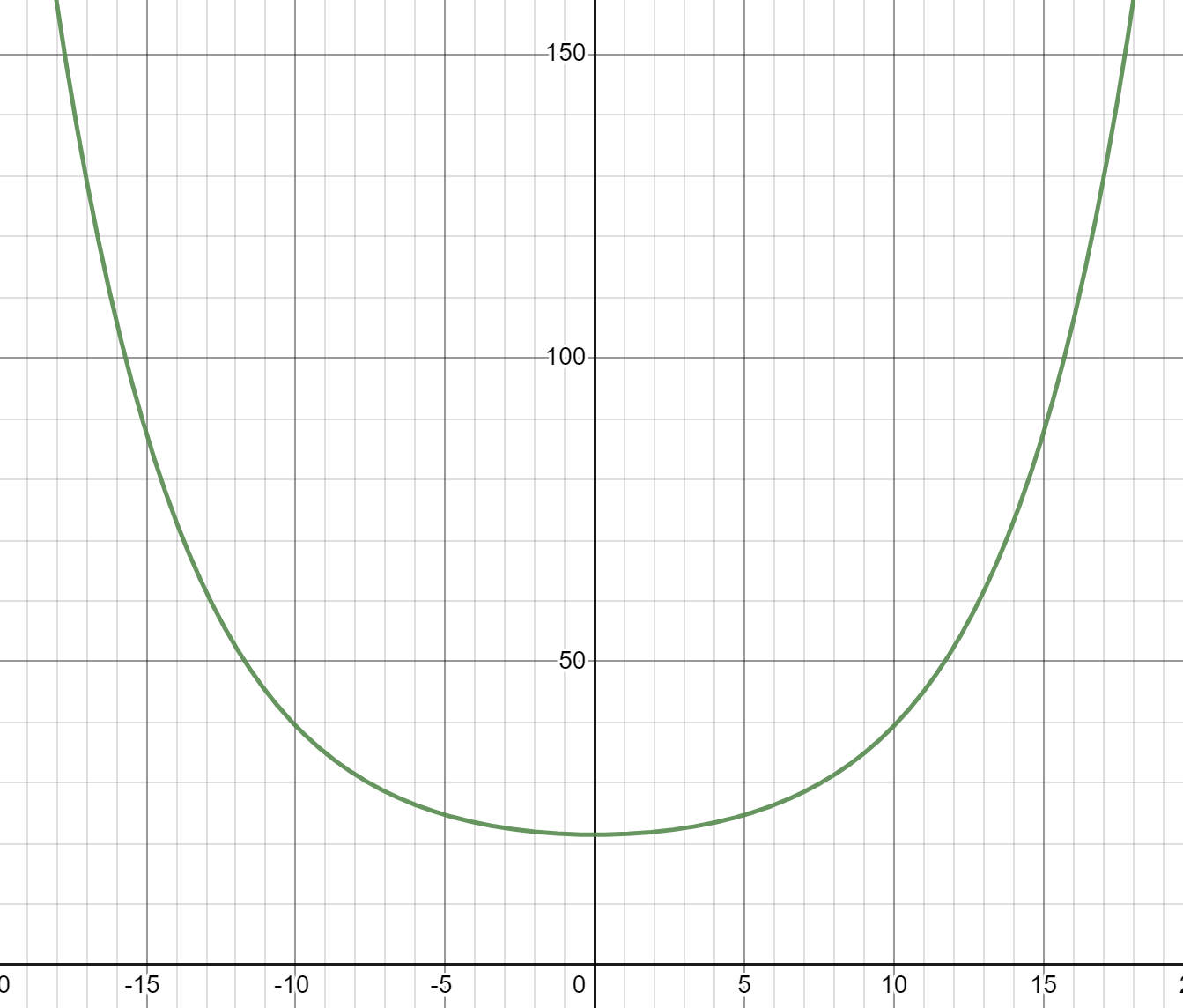
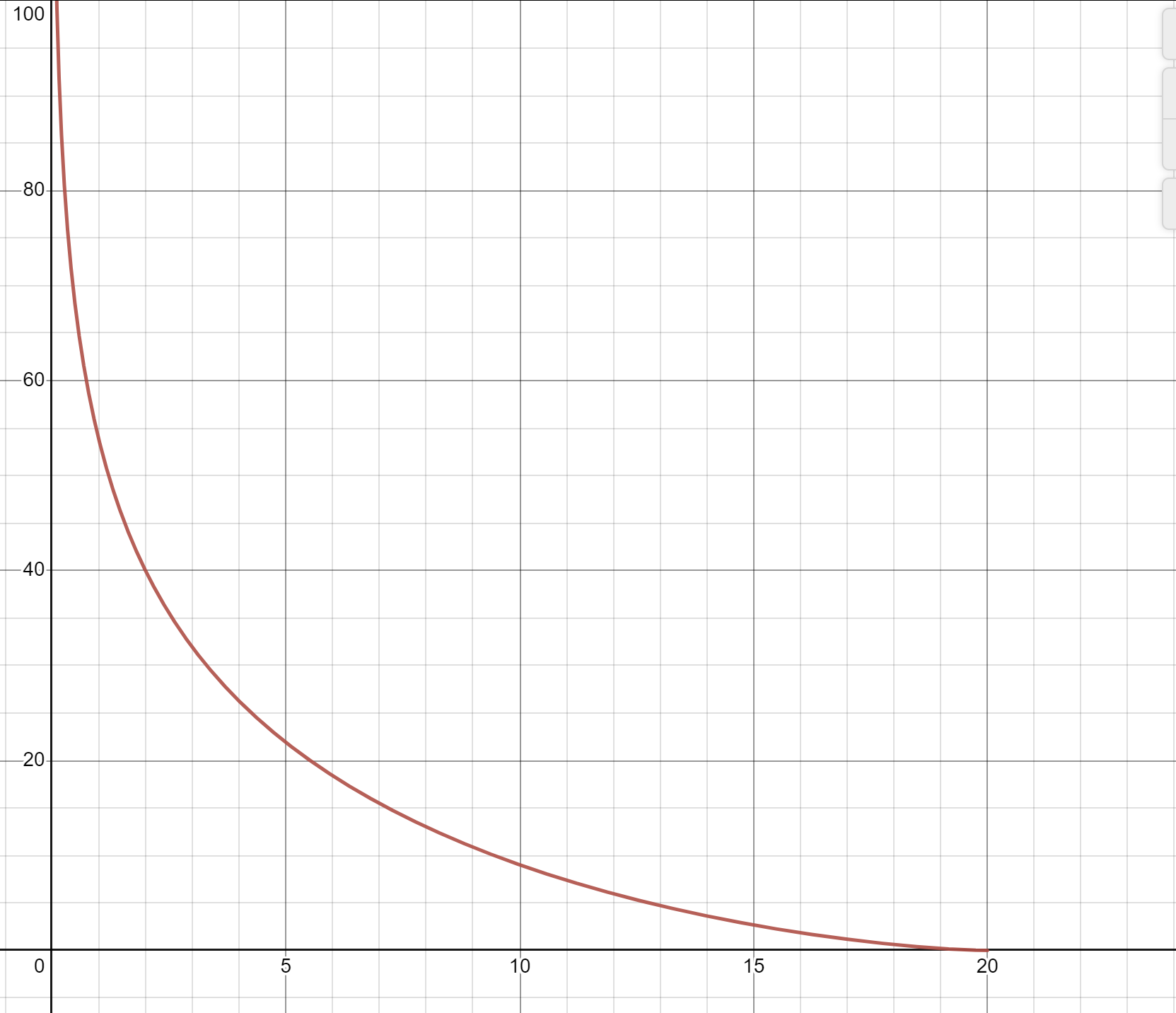
Newton’s Law of Cooling says that an object at temperature , when placed in an ambient environment at temperature , will cool according to the following differential equation:

where is some constant that depends on the properties of the object and environment.

Suppose you have a cup of hot black coffee and some creamer at room temperature. You are going to drink the coffee in 15 minutes, and you want it to be as hot as possible. Do you put the creamer in now, or wait until just before drinking?

(You should assume that the temperature taken on by a mixture of coffee and creamer is the average of their original temperatures, weighted by their original quantities.)