Examples

Trig sub in quadratic - completing the square

Compute the integral:

Solution

(1) Notice square root of a quadratic.

Complete the square to obtain Pythagorean form.

Find constant term for a complete square:

Add and subtract desired constant term:

Simplify:

---

(2) Perform shift substitution.

Set as inside the square:

Infer .

Plug into integrand:

---

(3)

Trig sub with .

Identify triangle:

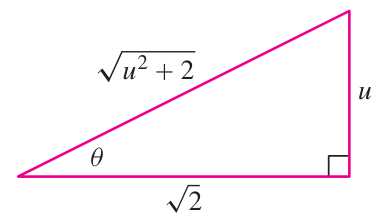
Use substitution . (From triangle or memorized tip.)

Infer .

Plug in data:

---

(4) Compute trig integral.

Use ad hoc formula:

---

(5) Convert trig back to .

First in terms of , referring to the triangle:

Then in terms of using .

Plug everything in:

---

(6) Simplify using log rules.

Log rule for division gives us:

The common denominator can be pulled outside as .

The new term can be “absorbed into the constant” (redefine ).

So we write our final answer thus: