Problems

01

Trig sub

Compute the definite integral:

Solution

04

(1) Substitute and thus . Adjust the bounds as follows:

Rewrite the integral:

---

(2) Use power-to-frequency conversion:

---

Note A: Use , then and this equals for .

Link to original

02

Trig sub

Compute the integral:

Solution

05

(1) Trig substitution. Notice , so we should make use of the identity .

Pick and thus .

Then:

Plug in:

(We assume that for the relevant values of .)

---

(2) Perform integration.

Either recall from memory, or multiply above and below by , and obtain:

---

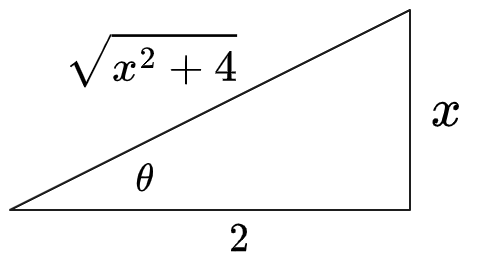
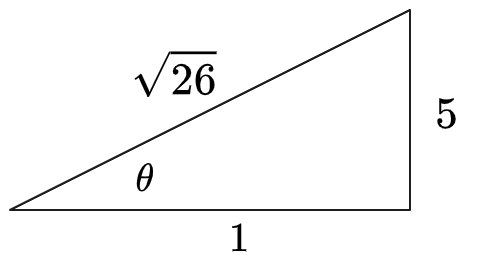
(3) To convert to we need given that .

Draw triangle expressing :

Therefore . We already know . Thus:

---

(4) Simplify with log rules:

Link to original

03

Trig sub

Compute the integral:

Solution

09

(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Plug in and simplify:

(We must assume that for the relevant values of here.)

---

(2) Use power-to-frequency conversion:

---

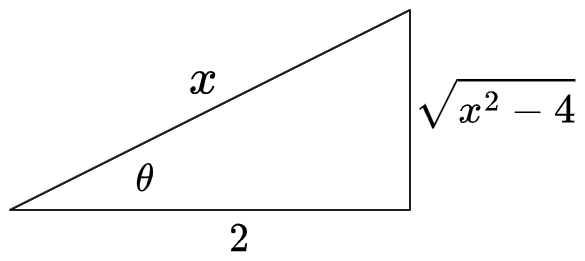
(3) Convert back to terms of :

First draw a triangle expressing :

Therefore:

For , use the double-angle identity:

Therefore:

Link to original

04

Trig sub

Compute the integral:

Hint: complete the square and then substitute.

Solution

10

(1) Complete the square:

---

(2) Substitute and thus :

---

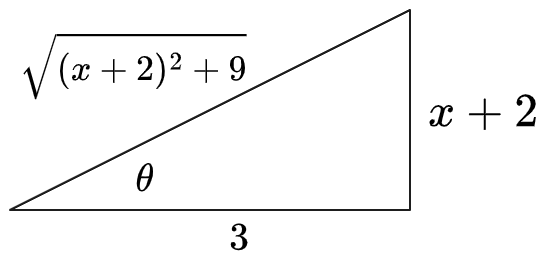
(3) Convert back to terms of :

First draw a triangle expressing :

It follows that . Then:

---

Note A: Using log rules, the denominator can be brought out as which can be “absorbed” into the constant .

Link to original

05

Trig sub

Compute the integral:

Solution

11

(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

---

(2) Convert to and integrate:

---

(3) Convert back to terms of :

Draw a triangle expressing :

Therefore and . Then:

Link to original

06

Double sub: -sub then trig sub

Compute the definite integral:

Solution

12

(1) Perform -sub setting and thus . Adjust the bounds as follows:

Therefore:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Adjust bounds:

Therefore:

---

(3) Integrate from memory or multiplying above and below by :

Link to original

07

Trig sub for electric charge

A charged wire lies on the -axis running from to . The electric field at the point is given by:

Find the numerical value of assuming and and and .

Solution

13

(1) Take out constants and insert given values:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Adjust bounds:

Then:

---

(3) Integrate:

---

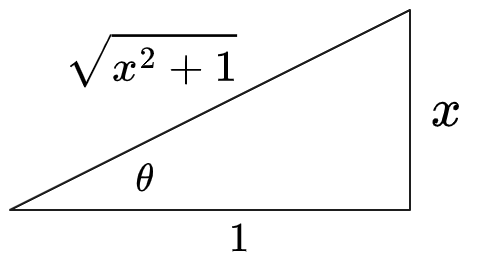
(4) Compute :

Draw a triangle expressing :

Therefore . Then:

Link to original