Theory

Theory 1

Certain algebraic expressions have a secret meaning that comes from the Pythagorean Theorem. This meaning has a very simple expression in terms of trig functions of a certain angle.

For example, consider the integral:

Now consider this triangle:

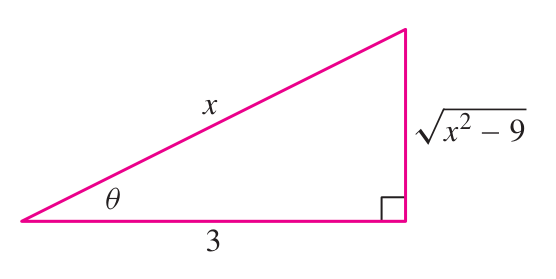
The triangle determines the relation , and it implies .

Now plug these into the integrand above:

Considering that , we obtain a very reasonable trig integral:

We must rewrite this in terms of using to finish the problem. We need to find assuming that . To do this, refer back to the triangle to see that . Plug this in for our final value of the integral:

Here is the moral of the story:

Re-express the Pythagorean expression using a triangle and a trig substitution.

In this way, square roots of quadratic polynomials can be eliminated.

There are always three steps for these trig sub problems:

• (1) Identify the trig sub: find the sides of a triangle and relevant angle .
• (2) Solve a trig integral (often a power product).
• (3) Refer back to the triangle to convert the answer back to .

To speed up your solution process for these problems, memorize these three transformations:

(1)

(2)

(3)

For a more complex quadratic with linear and constant terms, you will need to first complete the square for the quadratic and then do the trig substitution.