Theory

Theory 1

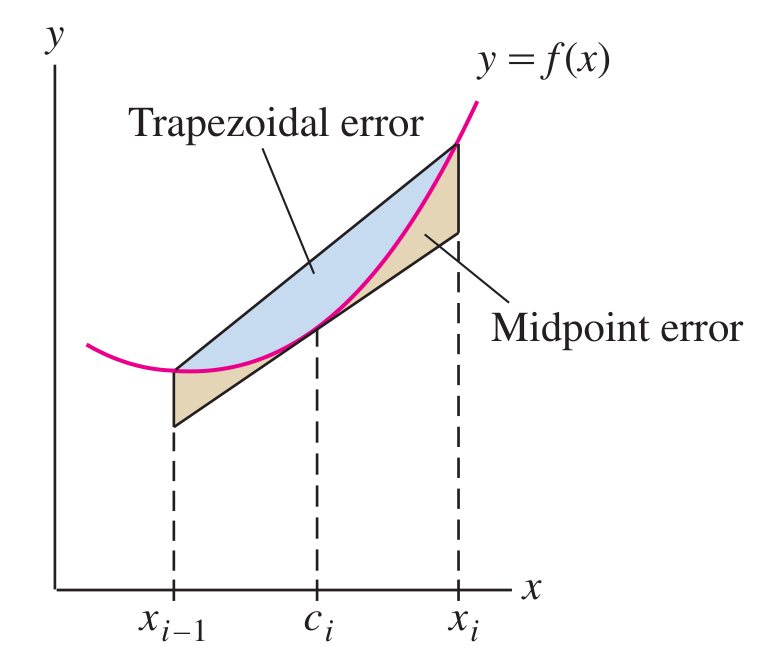
The Trapezoid Rule is a technique to approximate the area under a curve as the sum of areas of thin trapezoids whose top corners lie on the curve.

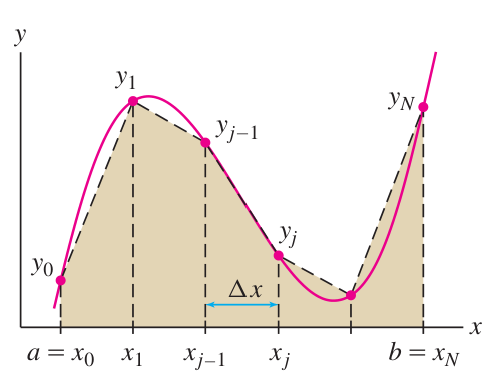The tops of the trapezoids are lines that approximate the curve. They are determined as lines that agree with the curve at two points.

Trapezoid rule - area formula

Given a function and a partition of the range labeled by (with and ), the Trapezoid Rule determines the area formula:

Notice the pattern in s and see how this formula comes about: The area of one trapezoid is . All vertical values (excepting the endpoints and ) are represented in two trapezoids, so their contribution is doubled.

Extra - Trapezoid rule - error bound

The error of the Trapezoid Rule approximation is bounded by this formula:

Here is any number satisfying for .

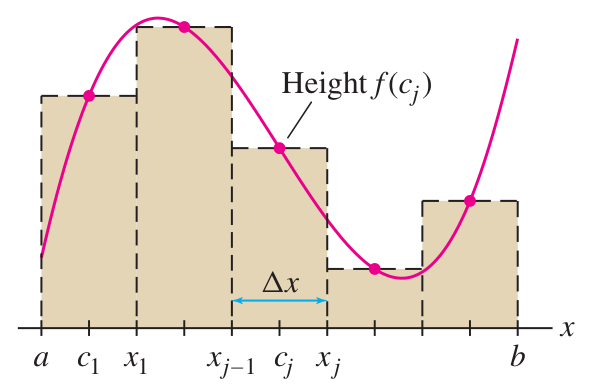
The Midpoint Rule is a technique to approximate the area under a curve as the sum of areas of thin rectangles whose top midpoints lies on the curve.

The very same formula also represents the areas of trapezoids whose top midpoints lie on the curve and whose top line is tangent to the curve:

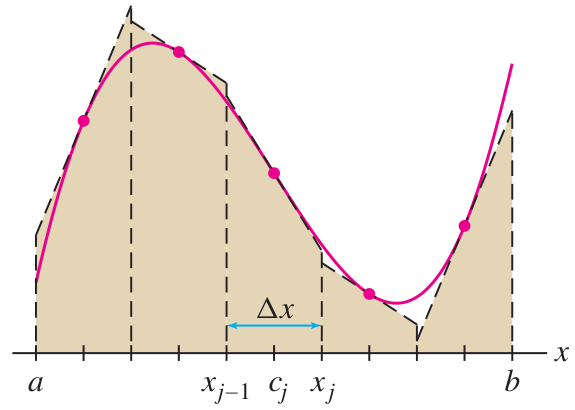
The reason they are equal is simple: when pivoting the top line on the ‘attached’ midpoint, the area of the trapezoid does not change.

Midpoint Rule - area formula

Given a function and a partition of the range labeled by (with and ), the Midpoint Rule determines the area formula:

Here each is the midpoint of the interval . It can be given by the formula .

Extra - Midpoint Rule - error bound

The error of the Midpoint Rule approximation is bounded by this formula:

Here is any number satisfying for .

Notice that has an error bound that is of the bound for . This does not mean that always has a smaller error than . It means that without calculating the error, simply plugging numbers into the error bound formulas, we obtain a smaller bound for than for . This is about our knowledge of the error, not the reality of the error.

Theory 2

It turns out that the Midpoint Rule and the Trapezoid Rule tend to differ from the exact integral in opposite directions, and the Midpoint Rule tends to be twice as accurate. Therefore we may improve on both of them by constructing a weighted average of the formulas. This is called Simpson’s Rule.

Simpson’s Rule - defining formula

Simpson’s Rule is given by the weighted sum of the Trapezoid and Midpoint Rules:

Simpson’s Rule - computing formula

Given a function and a partition of the range labeled by (with and ), Simpson’s Rule determines the area formula:

Note the pattern for Simpson’s Rule: 1, 4, 2, 4, 2, 4, 2, , 1

Simpson’s Rule - error bound

The error of Simpson’s Rule approximation is bounded by this formula:

Here is any number satisfying for .

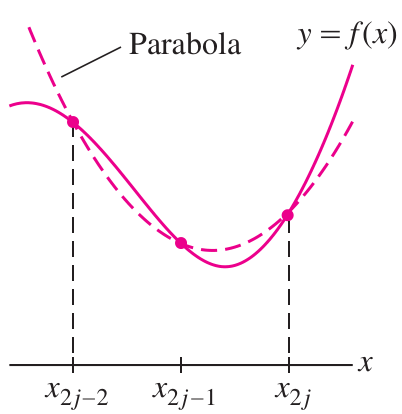
Simpson’s Rule “Parabola Rule”

The formula of Simpson’s Rule can also be explained or defined geometrically: it is the formula giving the sum of areas under small parabolas that meet the curve in three points.

There is a unique parabola passing through any three points with differing -values:

These may be pieced together to form an approximation to the curve: The area under the parabola through , , and is given by this formula:

This formula may be verified using basic calculus (area under a parabola) and a lot of algebra. (Ambitious students should derive it.)

The area under the parabola through , , and is given by a similar formula:

The Simpson’s Rule formula is the sum of all these formulas! So the s in Simpson’s come from duplication of endpoint terms as the “rectangular” regions are stacked end-to-end.