Arc length of chain, via position
A hanging chain describes a catenary shape. (‘Catenary’ is to hyperbolic trig as ‘sinusoid’ is to normal trig.) The graph of the hyperbolic cosine is a catenary:
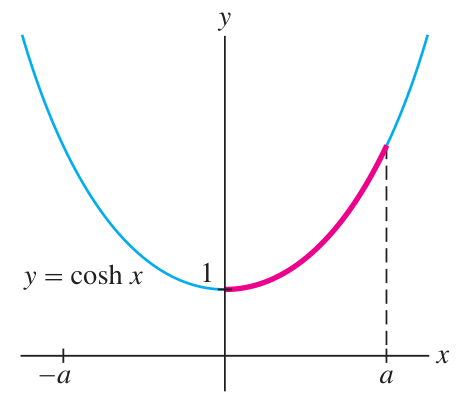
Let us compute the arc length of this catenary on the portion from
Solution
(1)
Arc-length formula.
Give arc length
(2) Compute
Hyperbolic trig derivative:
(3) Plug into formula.
Arc length:
(4) Hyperbolic trig identity.
Fundamental identity:
Rearrange:
(5) Plug into formula and compute.
Arc length:
Compute integral:
The arc length of a catenary curve matches the area under the catenary curve!