Theory 1
The total arc length of a curve is just the length of the curve.
The ‘arc length’ (not “total”) is a quantity measuring the length “as you go along,” usually given as a function of the points on the curve. It measures the length from some starting point ‘up to’ the given point.
We can use calculus to calculate the arc length of many curves. If the curve is the graph of a function, and we know the function and its derivative (whether from a formula or a data table), we can use integration to find the arc length.
Arc-length formula
The arc length
of the graph of over is: (This formula applies when
exists and is continuous on .) The arc length function
of the graph of , starting from , is:
Arc-length formula - explanation
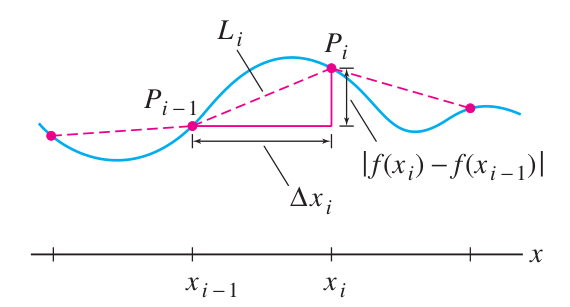
The arc-length integral is the limit of Riemann sums that add the lengths of straight line segments whose endpoints lie on the curve, and which together approximate the curve.
Each tiny line segment is the hypotenuse of a triangle with horizontal
and vertical . We can approximate the vertical
using the derivative: Considering infinitesimals in the limit, we have
(horizontal side) and (vertical side). The Pythagorean Theorem gives: which we can simplify using
: The integral of these infinitesimals gives the arc length: