Theory

Theory 1

The infinitesimal of arc length along a curve, , can be used to find the surface area of a surface of revolution. The circumference of an infinitesimal band is and the width of such a band is .

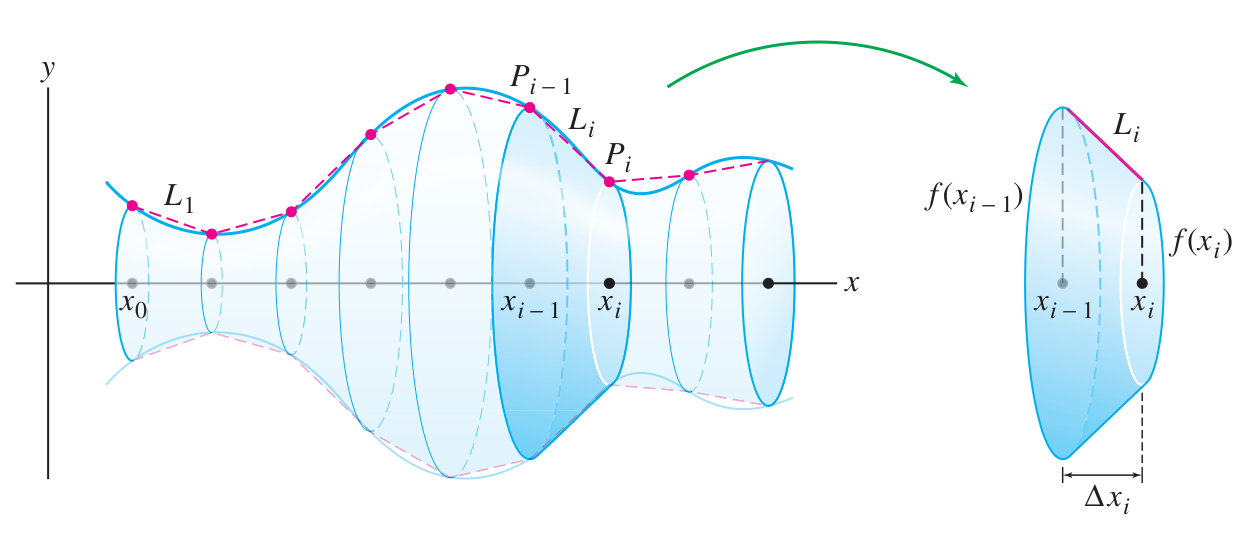
The general formula for the surface area is:

In any given problem we need to find the appropriate expressions for and in terms of the variable of integration. For regions rotated around the -axis, the variable will be ; for regions rotated about the -axis it will be .

Assuming the region is rotated around the -axis, and the cross section in the -plane is the graph of and so , the formula above becomes:

Area of revolution formula - thin bands

The surface area of the surface of revolution given by is given by the formula:

In this formula, we assume and is continuous. The surface is the revolution of on around the -axis.