01
Fluid force on a triangular plate
Find the total force on the submerged vertical plate that is an isosceles triangle with (bottom) base
and height , and assume it is submerged with the upper vertex below the surface. Liquid is oil with density .
Solution
01
(1) Integral formula:
(2) Integrand components:
Width function:
Depth function:
(3) Integrate:
Link to original
02
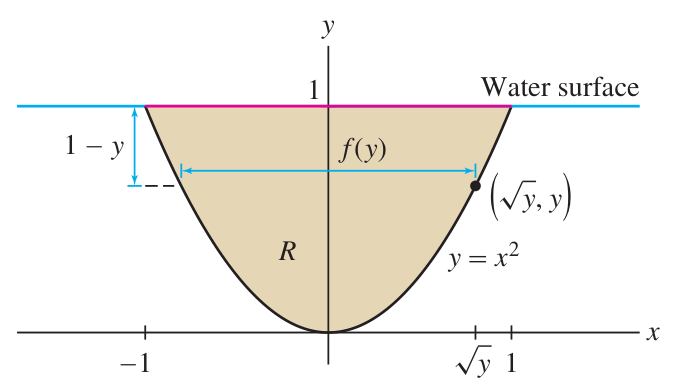
Fluid force on a parabolic plate
A parabolic plate is submerged vertically in water as in the figure:
The shape of the plate is bounded below by
and above by the line . (Note that increases going up in this coordinate system.) Compute the total fluid force on this plate.
(Hint: your integrand should contain
as a factor.)
Solution
05
(1) Integral formula:
(2) Integrand components:
So we have:
(3) Integrate:
(Assuming
Link to originaland .)
03
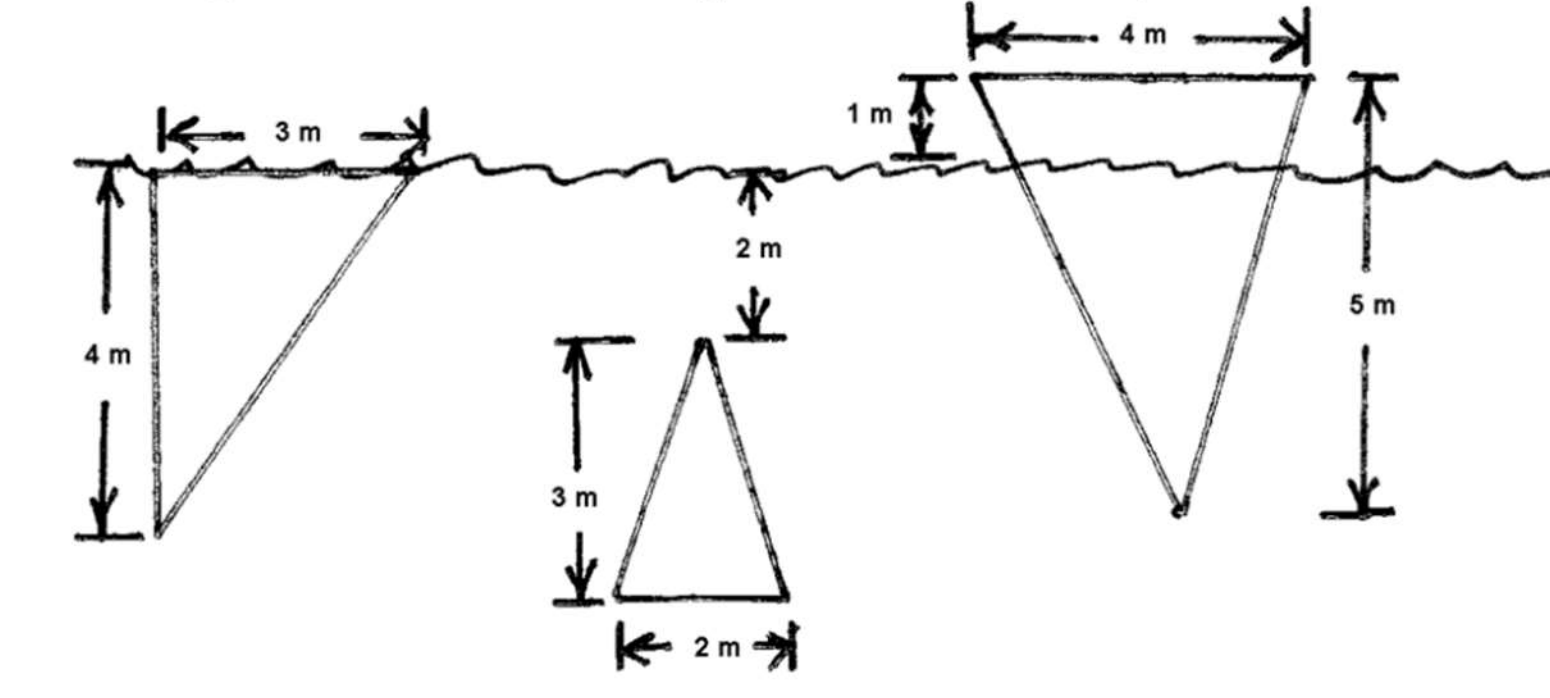
Fluid force on triangular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
06
(1) Integral formula:
Option 1:
(2) Using
at water line, increasing downwards: (a) Left: (b) Center:
(c) Right:
Option 2:
(2) Using
at top of shape, increasing downwards: (a) Left: (b) Center:
(c) Right:
Link to original
04
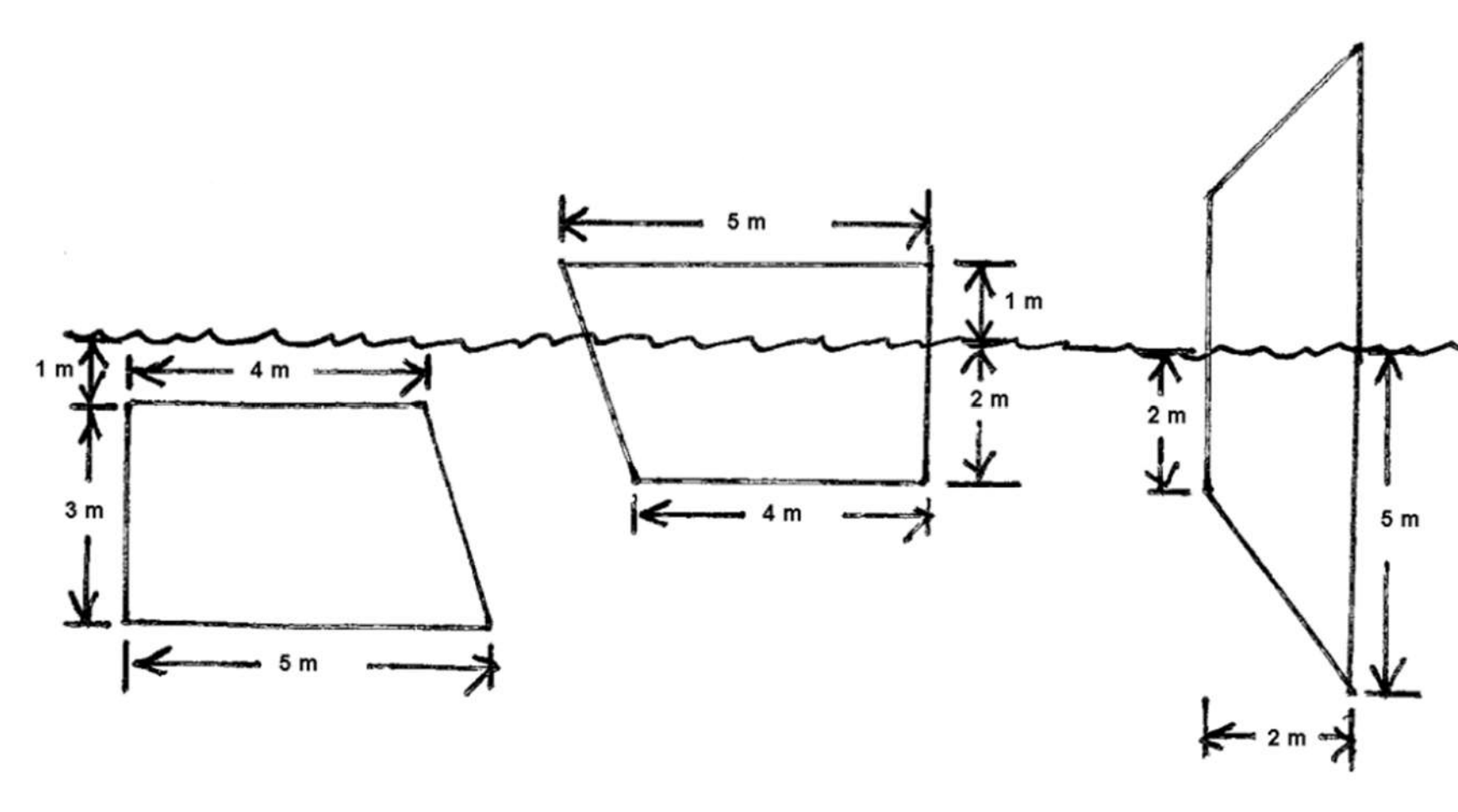
Fluid force on trapezoidal plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
02
(a) Left:
Set
at the water line, increasing downwards. Alternative: set
at the top of the trapezoid. Obtain:
(b) Center:
Set
at the water line, increasing downwards. Alternative: set
at the top of the trapezoid. Obtain:
(c) Right:
Set
at the water line, increasing downwards. Link to original
05
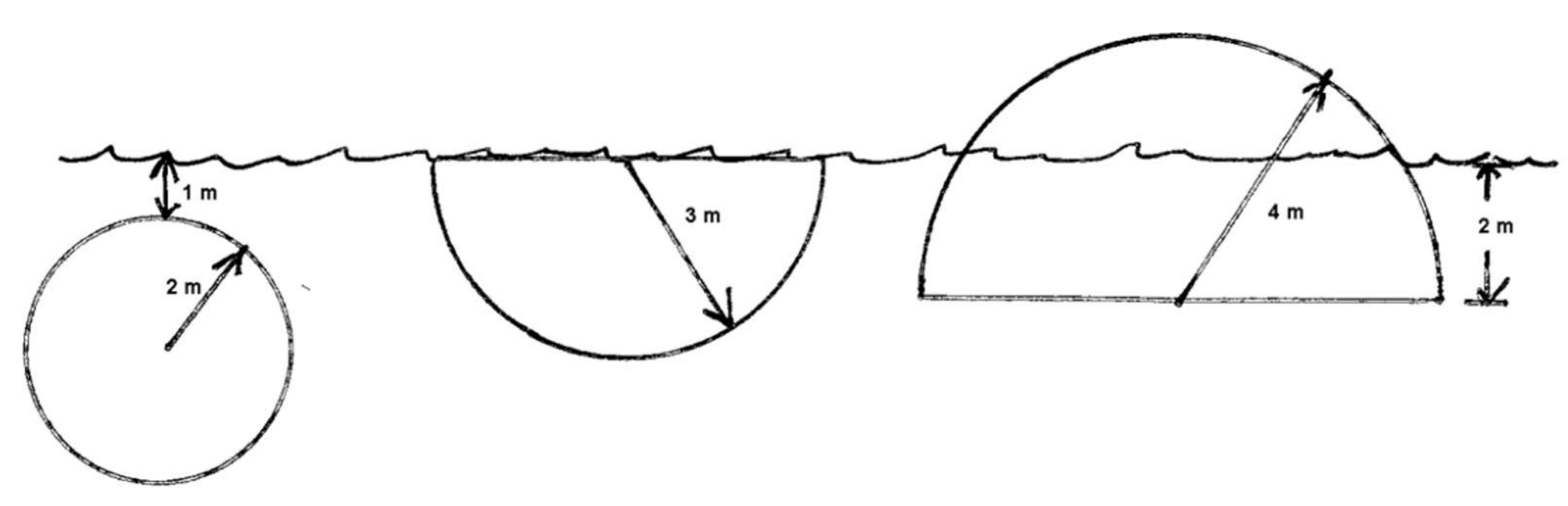
Fluid force on circular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
07
(1) Integral formula:
Option 1:
(2) Using
at water line, increasing downwards: (a) Left: (b) Center:
(c) Right:
Option 2:
(2) Using
at center of shape, increasing downwards: (a) Left: (b) Center:
(c) Right:
Link to original