McMillan Math
Home

Examples

CoM of a parabolic plate

Find the CoM of the region depicted:

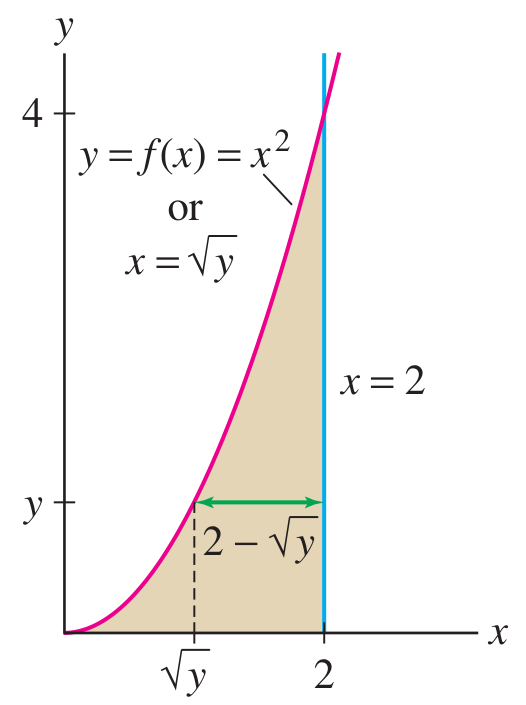
center

Solution

(1) Compute the total mass:

Area under the curve with density factor :

(2) Compute :

Formula:

Interpret and calculate:

(3) Compute :

Formula:

Width of horizontal strips between the curves:

Interpret :

Calculate integral:

(4) Compute CoM coordinates from moments:

CoM formulas:

Insert data:

Computing CoM using only vertical strips

Find the CoM of the region:

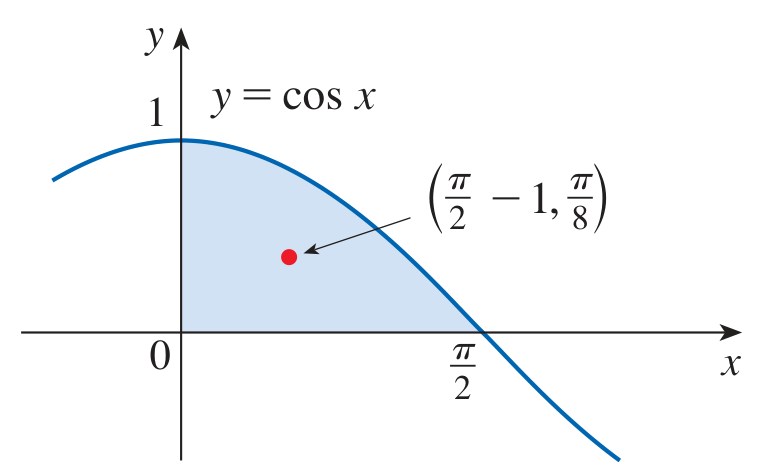
center

Solution

(1) Compute the total mass :

Area under the curve times density :

(2) Compute using vertical strips:

Plug into formula:

Integration by parts. Set , and so , :

(3) Compute , also using vertical strips:

Plug and into formula:

Integration by ‘power to frequency conversion’:

(4) Compute CoM:

CoM formulas:

Plug in data:

CoM of region between line and parabola

Compute the CoM of the region below and above with .

Solution

(1) Compute total mass :

Name the functions: (lower) and (upper) over .

Mass is area (between curves) times density:

(2) Compute using vertical strips:

(3) Compute also using vertical strips:

(4) Compute CoM using moment formulas:

Center of mass using moments and symmetry

Find the center of mass of the two-part region:

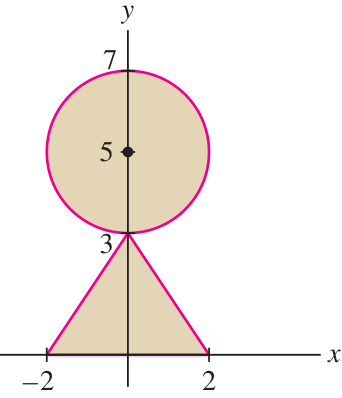
center

Solution

(1) Symmetry: CoM on -axis

Because the region is symmetric in the -axis, the CoM must lie on that axis. Therefore .

(2) Additivity of moments:

Write for the total -moment (distance measured to the -axis from above).

Write and for the -moments of the triangle and circle.

Additivity of moments equation:

(3) Find moment of the circle :

By symmetry we know .

By symmetry we know .

Area of circle with is , so total mass is .

Centroid-from-moments equation:

Solve the equation for :

(4) Find moment of the triangle using integral formula:

Similar triangles:

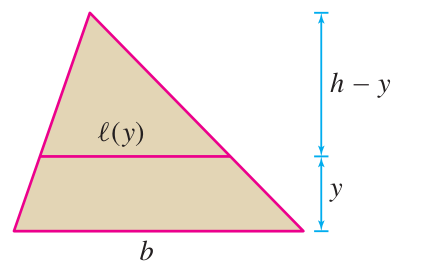center Quick linear interpolation function:

Thus:

Conclude:

(5) Apply additivity:

(6) Total mass of region:

Area of circle is . Area of triangle is . Thus .

(7) Compute center of mass from total and total :

We have and . Plug into formula:

Center of mass - two part region

Find the center of mass of the region which combines a rectangle and triangle (as in the figure) by computing separate moments. What are those separate moments? Assume the mass density is .

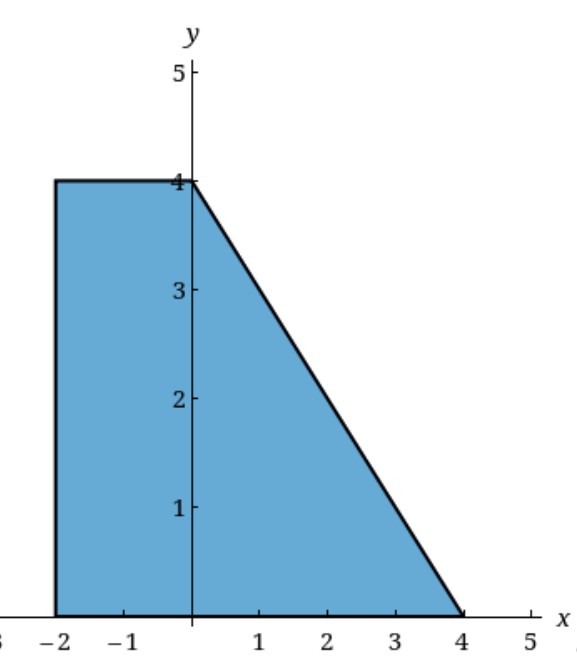
center

Solution

(1) Apply symmetry to rectangle:

By symmetry, the center of mass of the rectangle is located at .

Thus and .

(2) Find moments of the rectangle:

Total mass of rectangle . Thus:

(3) Find moments of the triangle:

Area of vertical slice . Distance from -axis . Total integral:

Total integral:

(4) Add up total moments:

General formulas: and

Plug in data: and

(5) Find center of mass from moments:

Total mass of triangle .

Total combined mass .

Apply moment relation: