01
Center of mass of a house
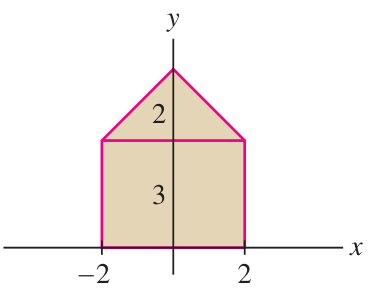
A “house” is the region bounded by the (non-regular) pentagon with vertex points at
, , , , . Find the CoM of the house using additivity of moments.
Solution
01
(1) Compute masses:
(2) Consider symmetries of rectangle:
Therefore
and: Therefore:
(3) Consider symmetry of triangle:
(4) Compute
by integration:
(5) Optional step: infer
:
(6) Additivity of moments:
(7) Compute CoM:
Thus:
Link to original
02
CoM of region between curves
Find the CoM of the region between the graph of
and the graph of over .
Solution
02
Option 1: In terms of
. (1) Mass of region:
(2) Integral formula for
:
(3) Integral formula for
:
(4) Compute
:
Option 2: In terms of
. (1) Mass:
(2)
:
(3)
: Link to original
03
FlatCoMMan
Find the center of mass of FlatCoMMan. Assume a constant mass density
. Use additivity of moments.
Solution
04
Assume
for all of these. The value of
does not affect the CoM point if is a constant. Region 1:
Region 2:
Region 3:
Region 4:
Region 5:
Region 6:
Region 7:
FlatCoMMan:
Link to original
04
CoM from Simpson’s
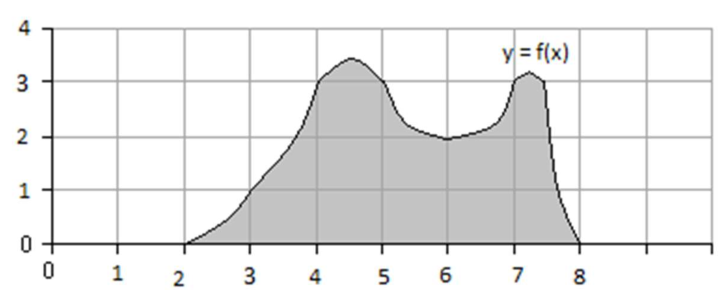
Use Simpson’s rule (with 6 subintervals) to estimate the centroid of this region:
You will need to estimate
and and with three separate integrals. You can use a calculator for your arithmetic.
Solution
05
(1) Simpson’s Rule formula:
(2) Simpson’s for total mass
: Therefore:
So:
(3) Simpson’s for moment to
-axis: Integral formula:
Approximate with
:
(4) Simpson’s for moment to
-axis: Integral formula:
Approximate with
:
(5) Compute CoM:
Link to original