Theory

Theory 1

Moment

The moment of a region to an axis is the total (integral) of mass times distance to that axis:

Moment to :

Moment to :

Notice the swap in letters

• integrand has factor
• integrand has factor

Notice the total mass

If you remove or factors from the integrands, the integrals give total mass .

These formulas are obtained by slicing the region into rectangular strips that are parallel to the axis in question.

The area per strip is then:

• — region under
• — region between and
• — region ‘under’
• — region between and

---

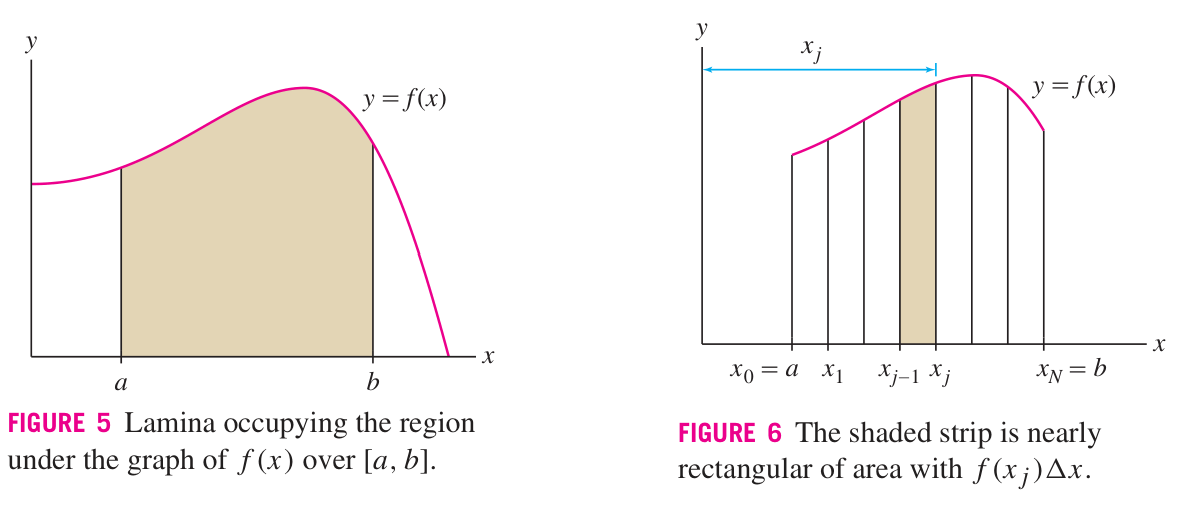
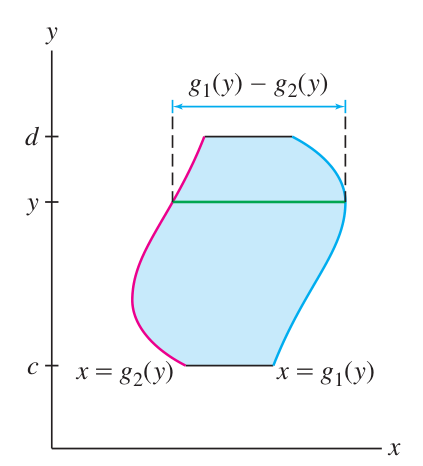
The idea of moment is related to:

• Torque balance and angular inertia
• Center of mass

The center of mass (CoM) of a solid body is a single point with two important properties:

1. “average position” of the body
   • The average position determines an effective center of dynamics. For example, gravity acting on every bit of mass of a rigid body acts the same as a force on the CoM alone.
2. “balance point” of the body
   • The net torque (rotational force) about the CoM, generated by a force distributed over the body’s mass, equivalently a force on the CoM, is zero.

Centroid

When the body has uniform density, then the CoM is also called the centroid.

---

Center of mass from moments

Coordinates of the CoM:

Here is the total mass of the body.

Center of mass from moments - explanation

Notice how these formulas work. The total mass is always . The moment to (for example) is . Dividing these two values:

where .

In other words, through the formula , we find that is the average value of over the region with area .

Theory 2

A downside of the technique above is that to find we needed to convert the region into functions in . This would be hard to do if the region was given as the area under a curve but cannot be found analytically. An alternative formula can help in this situation.

Midpoint of strips for opposite variables

When the region lies between and , we can find with an -integral:

When the region lies between and , we can find with a -integral:

Region under a curve

For the region “under the curve” , just set:

For the region “under the curve” , set:

The idea for these formulas is to treat each vertical strip as a point concentrated at the CoM of the vertical strip itself.

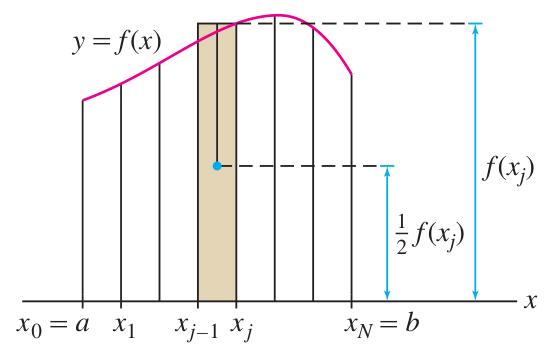
The height to this midpoint is , and the area of the strip is , so the integral becomes .

Midpoint of strips formula - full explanation

• If the strip is located at some , with values from up to , then:

• The area of the strip is . So the integral formula for can be recast:

• If the vertical strips are between and , then the midpoints of the strips are given by the ‘average’ function:

• The height of each strip is , so .
• Putting this together:

Theory 3

Two useful techniques for calculating moments and (thereby) CoMs:

• Additivity principle
• Symmetry

Additivity says that you can add moments of parts of a region to get the total moment of the region (to a given axis).

A symmetry principle is that if a region is mirror symmetric across some line, then the CoM must lie on that line.