01
Pumping water from hemispherical tank
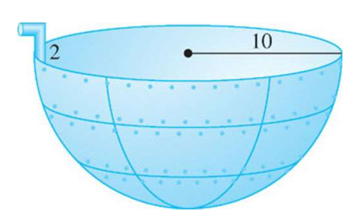
A hemispherical tank (radius
) is full of water. A pipe allows water to be pumped out, but requires pumping up above the top of the tank.
(a) Set up an integral that expresses the total work required to pump all the water out of the tank, assuming it is completely full.
(b) Now assume the tank start out full just to
. What does the integral become?
Solution
03
(a) (1) Integral formula:
(2) Setup:
Coordinate system: set
at the top of the tank, increasing downwards. Horizontal slice of the tank: disk of radius
at depth , satisfies: Distance pumped up (add
for the spigot): Thus:
(b) (1) Change upper bound, top of water at
: Link to original
02
Building a conical tower
Set up an integral that expresses the work done (against gravity) to build a circular cone-shaped tower of height
and base radius out of a material with mass density .
Solution
04
(1) Integral formula:
Option 1: (2) Setup:
Set
at the bottom, increasing upwards. Radius of the cone with a QLIF:
Horizontal slice of the cone tower: disk of radius
at height , satisfies: The slice at
is raised a distance of . Thus:
Option 2: (2) Setup:
Set
at the top of the cone, increasing downwards. Now
is the distance from the ground up to the height of a slice indexed by . Radius function:
Thus:
Link to original
03
Work to raise a leaky bucket
A bucket of water is raised by a chain to the top of a
-foot building. The water is leaking out, and the chain is getting lighter. The bucket weighs
, the initial water weighs , and the chain weighs , and the water is leaking at a rate of as the bucket is lifted at a constant rate of . What is the total work required to raise the bucket of water?
Solution
08
(1) Integral formula:
Let
at the ground and increase going up.
(2) Compute force:
The force on the rope (at the top) when the bucket is at height
is: We know
. Water is leaking at
. Therefore: The weight of chain remaining is:
Put together:
(3) Integrate:
Link to original
04
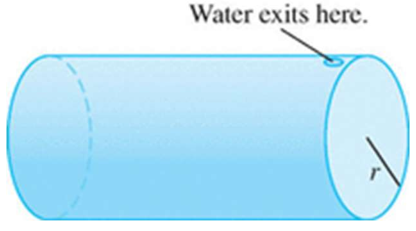
Work to pump water from cylindrical tank
A cylindrical tank is full of water and the water is pumped out the top. (See figure.) The length of the tank is
and the radius is .
(a) Set up an integral for the total work performed assuming the tank is initially completely full.
(b) Set up an integral for the total work performed assuming the tank is initially full to
and the water is pumped out of a spigot extending above the top of the tank.
Solution
09
(1) Integral formula:
Set
at the center of the tank.
(a) (2) Geometry:
So:
Tank length is
so a horizontal slice is a rectangle with area . Depth is:
Therefore:
(b) (2) Change bounds and height:
Link to original
05
Work to build a pyramid
The Great Pyramid of Giza is
tall and has a square base with on each side. It is built of stone with mass density . Set up an integral that expresses the work (against gravity) required to build the pyramid.
Solution
10
(1) Integral formula:
(2) Integrand components:
Option 1: Set
at the base, going up. Take a cross-sectional slice with a vertical plane. This intersects the surface of the pyramid in a triangle whose width
is the side length of the square (the horizontal cross section) at height . Note that
. So we have:
Option 2:
Set
at the vertex, going down. And:
Link to original