Problems

01

General term of a series

Write this series in summation notation:

$$\frac{1}{1}-\frac{2^2}{2\cdot 1}+\frac{3^3}{3\cdot 2\cdot 1}-\frac{4^4}{4\cdot 3\cdot 2\cdot 1}+\cdots$$

(Hint: Find a formula for the general term $a_n$.)

02

Geometric series

Compute the following summation values using the sum formula for geometric series.

(a) ${\displaystyle \sum _{n=0}^{\infty }{5}^{-n}}$ $$ (b) ${\displaystyle \sum _{n=0}^{\infty }\frac{2+3^n}{5^n}}$

03

Geometric series

Compute the following summation values using the sum formula for geometric series.

(a) ${\displaystyle \sum _{n=-4}^{\infty }{(-\frac{4}{9})}^n}$ $$ (b) ${\displaystyle \sum _{n=0}^{\infty }{e}^{3-2n}}$

04

Repeating digits

Using the geometric series formula, find the fractional forms of these decimal numbers:

(a) $0.\bar{2}=0.222222\dots$ $$ (b) $0.4\bar{9}=0.4999999\dots$

05

Series from its partial sums

Suppose we know that the partial sums $S_N$ of a series $S={\sum }_{n=1}^{\infty }{a}_n$ are given by the formula $S_N=5-\frac{2}{N^2}$.

(a) Compute $a_3$.

(b) Find a formula for the general term $a_n$.

(c) Find the sum $S$.

06

Partial sums and total sum

Consider the series:

$$\sum _{n=1}^{\infty }\frac{{(-8)}^{n-1}}{9^n}$$

(a) Compute a formula for the $N^{\text{th}}$ partial sum $S_N$ by applying the “shift method” steps using the values in this series.

(b) By taking the limit of this formula as $N\to \infty$, find the value of the series.

(c) Find the same value of the series by computing $a_0$ and $r$ and plugging into $S=\frac{a_0}{1-r}$.

07

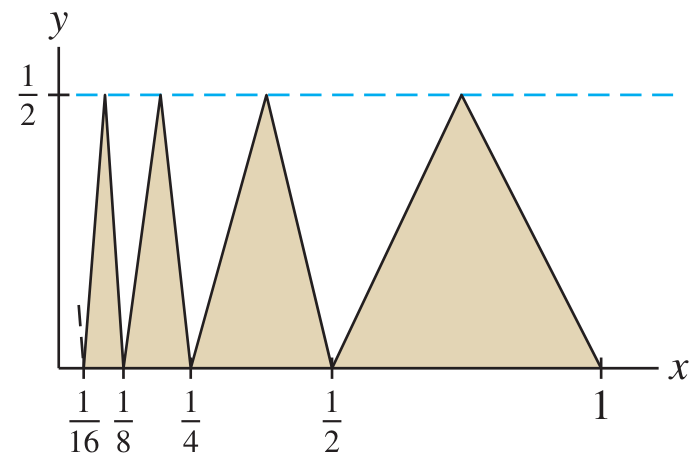
Total area of infinitely many triangles

Find the area of all the triangles as in the figure:

(The first triangle from the right starts at $1$, and going left they never end.)