Theory

Theory 1

A sequence has a limit if its terms tend toward a specific number, or toward .

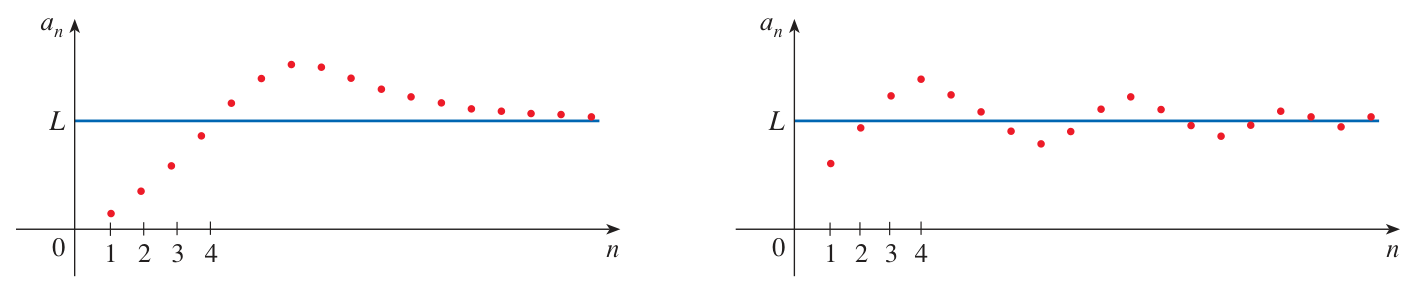
When this happens we can write “” with some number or . We can also write “ as ”.

The sequence is said to converge if it has a finite limit .

Some sequences don’t have a limit at all, like :

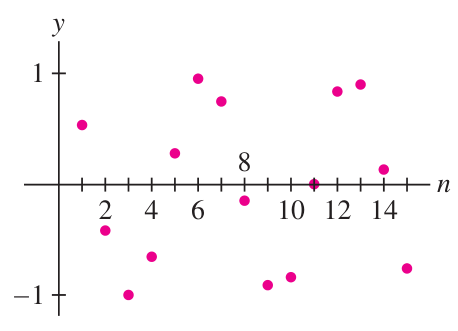
Or :

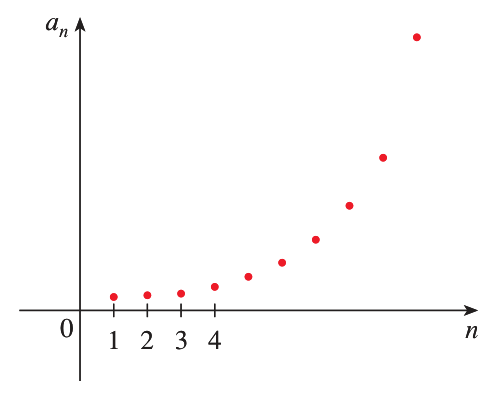
These sequences diverge. In the second case, there is a limit , so we say it diverges to .

A sequence may have a limit of but is still said to diverge.

Extra - Convergence definition

The precise meaning of convergence is this. We have as if, given any proposed error , it is possible to find such that for all we have .

When , convergence means that given any , we can find such that for all we have .

Similarly for .

---

If the general term is a continuous function of , we can replace with the continuous variable and compute the continuous limit instead:

If would be a differentiable function, and we discover an indeterminate form, then we can apply L’Hopital’s Rule to find the limit value. For example, if the indeterminate form is , we can convert it to and apply L’Hopital.

Theory 2

Monotone sequences

A sequence is called monotone increasing if for every .

A sequence is called monotone decreasing if for every .

In this context, ‘monotone’ just means it preserves the increasing or decreasing modality for all terms.

Monotonicity Theorem

If a sequence is monotone increasing, and bounded above by , then it must converge to some limit , and .

If a sequence is monotone decreasing, and bounded below by , then it must converge to some limit , and .

Terminology:

• Bounded above by means that for every
• Bounded below by means that for every

Notice!

The Monotonicity Theorem says that a limit exists, but it does not provide the limit value.

Theory 3

Series convergence

We say that a series converges when its partial sum sequence converges:

Let us apply this to the geometric series. Recall our formula for the partial sums:

Rewrite this formula:

Now take the limit as :

So we see that converges exactly when . It converges to .

(If then the denominator is , and if then the factor does not converge.)

Furthermore, we have the limit value:

This result confirms the formula we derived for the total for a geometric series. This time we did not start by assuming exists, on the contrary we proved that exists. (Provided that .)

Extra - Aspects of and from the geometric series

Notice that we always have the rule:

This rule can be viewed as coming from partitioning the full series into a finite part and the remaining infinite part:

We can remove a factor from the infinite part:

The parenthetical expression is equal to , so we have the formula given above.