Examples

Parametric circles

The standard equation of a circle of radius centered at the point :

This equation says that the distance from a point on the circle to the center point equals . This fact defines the circle.

Parametric coordinates for the circle:

For example, the unit circle is parametrized by and .

Parametric lines

(1) Parametric coordinate functions for a line:

Compare this to the graph of linear function:

Vertical lines cannot be described as the graph of a function. We must use .

---

(2) Parametric lines can describe all lines equally well, including horizontal and vertical lines.

A vertical line is achieved by setting and .

A horizontal line is achieved by setting and .

A non-vertical line may be achieved by setting and , and .

---

(3) Assuming that , the parametric coordinate functions describe a line satisfying:

and therefore the slope is and the -intercept is .

---

(4) The point-slope construction of a line has a parametric analogue:

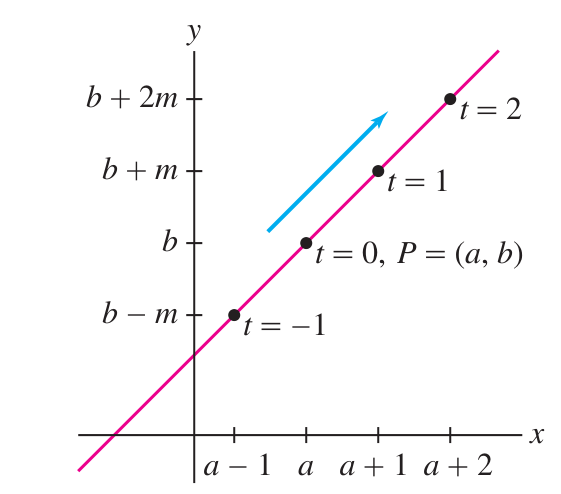
Parametric ellipses

The general equation of an ellipse centered at with half-axes and is:

This equation represents a stretched unit circle:

• by in the -axis
• by in the -axis

Parametric coordinate functions for the general ellipse:

Parametric cycloids

The cycloid is the curve traced by a pen attached to the rim of a wheel as it rolls.

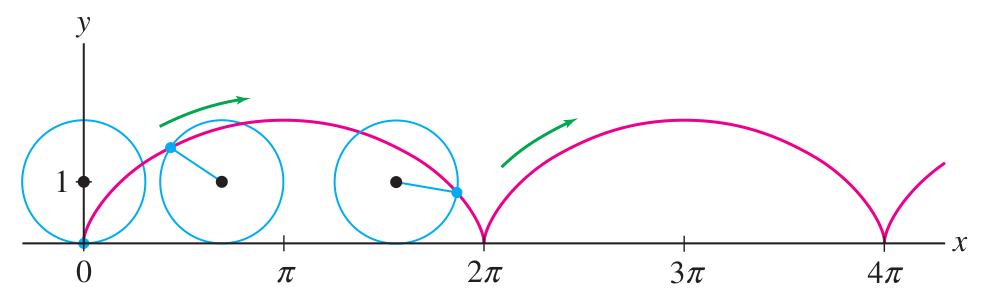
It is easy to describe the cycloid parametrically. Consider the geometry of the situation:

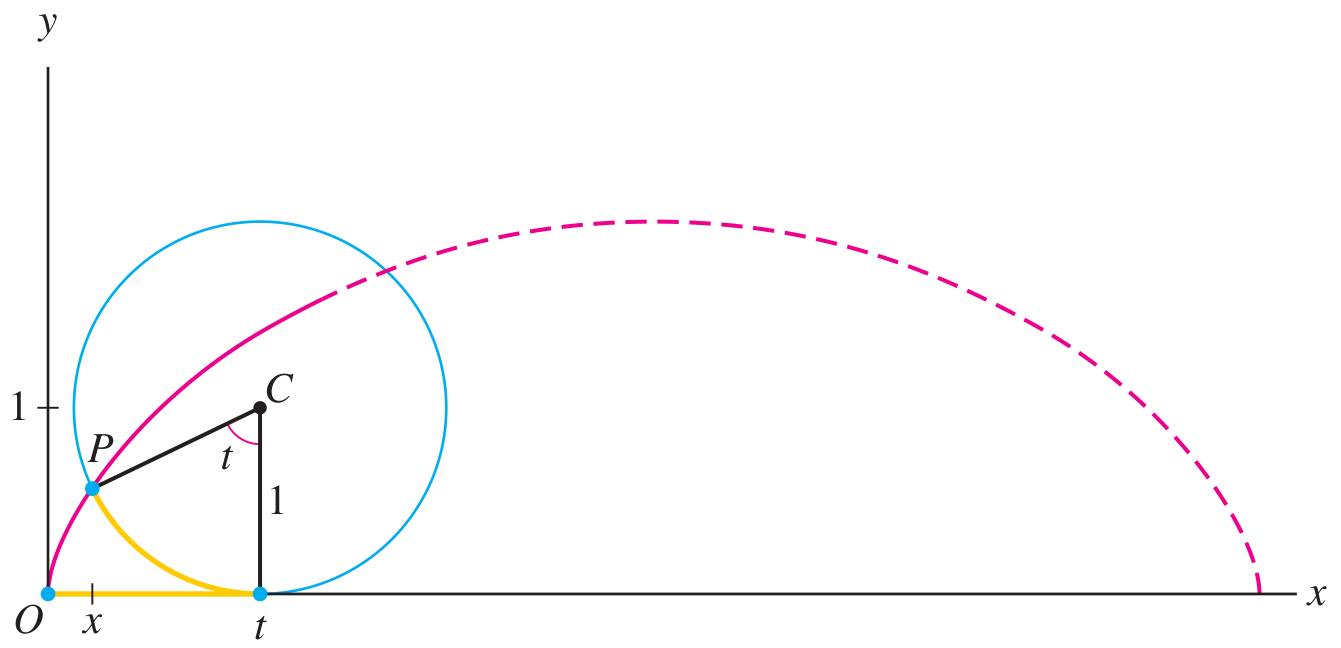
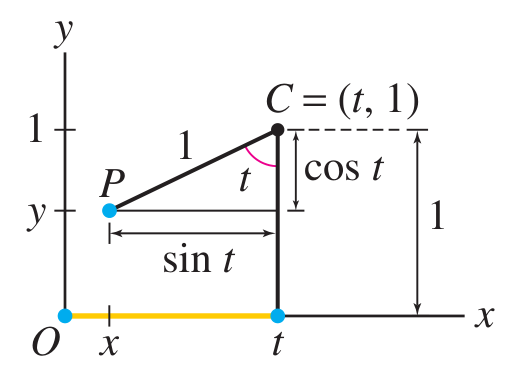
The center of the wheel is moving rightwards at a constant speed of , so its position is . The angle is revolving at the same constant rate of (in radians) because the radius is .

The triangle shown has base , so the coordinate is . The coordinate is .

So the coordinates of the point are given parametrically by:

If the circle has another radius, say , then the parametric formulas change to: