Theory

Theory 1

Parametric curves are curves traced by the path of a ‘moving’ point. An independent parameter, such as for ‘time’, controls both and values through Cartesian coordinate functions and . The coordinates of the moving point are .

Parametric curve

A parametric curve is a function from parameter space to the plane given in terms of coordinate functions:

Other notations

Be aware that sometimes the coordinate functions are written with and (or yet other letters) like this:

Or simply equating coordinate letters with functions:

Sometimes a different parameter is used, like or .

For example, suppose:

The curve traced out is a parabola that opens horizontally:

---

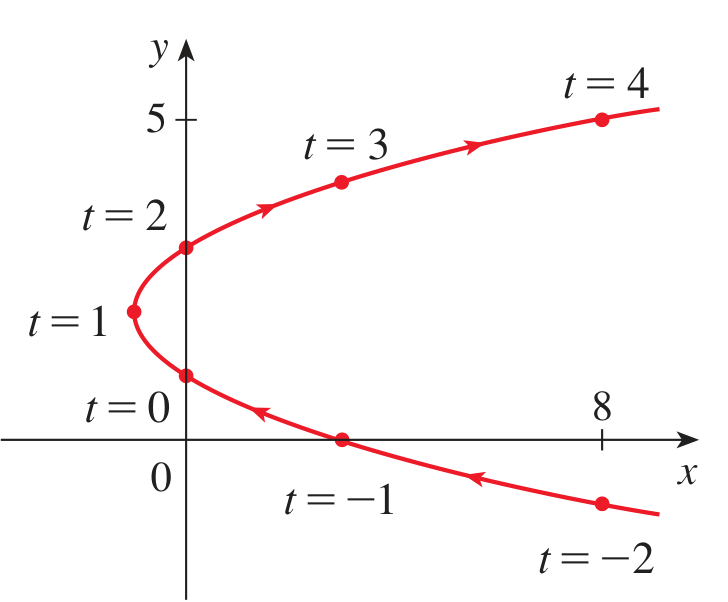
Given a parametric curve, we can create an equation satisfied by and variables by solving for in either coordinate function (inverting either or ) and plugging the result into the other function.

In the example:

This is the equation of a parabola centered at that opens to the right.

Image of a parametric curve

The image of a parametric curve is the set of output points that are traversed by the moving point.

A parametric curve has hidden information that isn’t contained in the image:

• The time values when the moving point is found in various locations.
• The speed at which the curve is traversed.
• The direction in which the curve is traversed.

---

We can reparametrize a parametric curve to use a different parameter or different coordinate functions while leaving the image unchanged.

In the previous example, shift by :

Since the parameter and the parameter both cover the same values for , the same curve is traversed. But the moving point in the second, shifted version reaches any given location one unit earlier in time. (When in the second version, the input to and is the same as when in the first one.)