Theory

Theory 1

Polar coordinates are pairs of numbers which identify points in the plane in terms of distance to origin and angle from -axis:

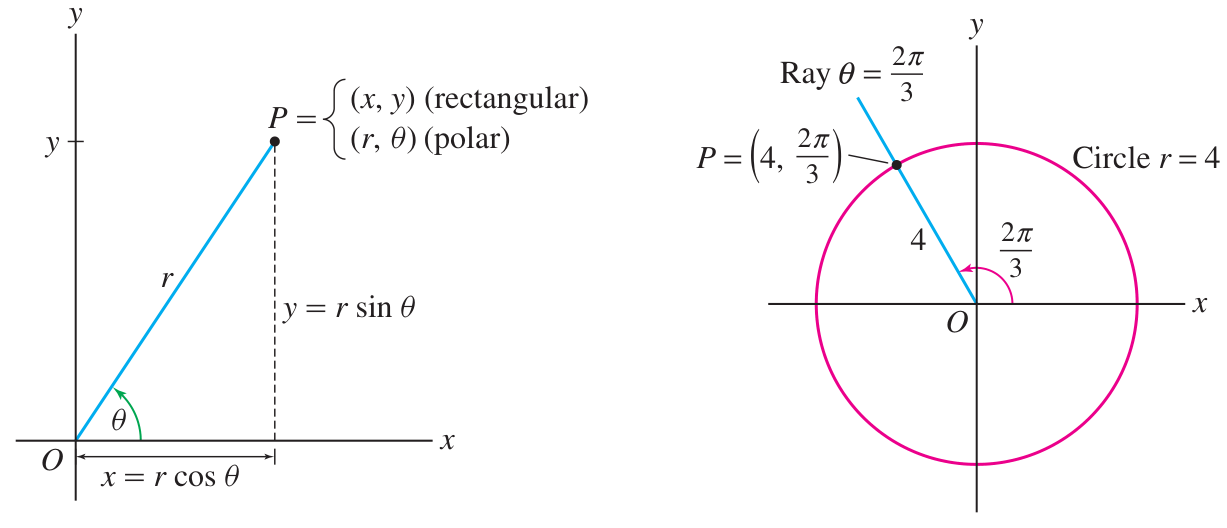
Converting

---

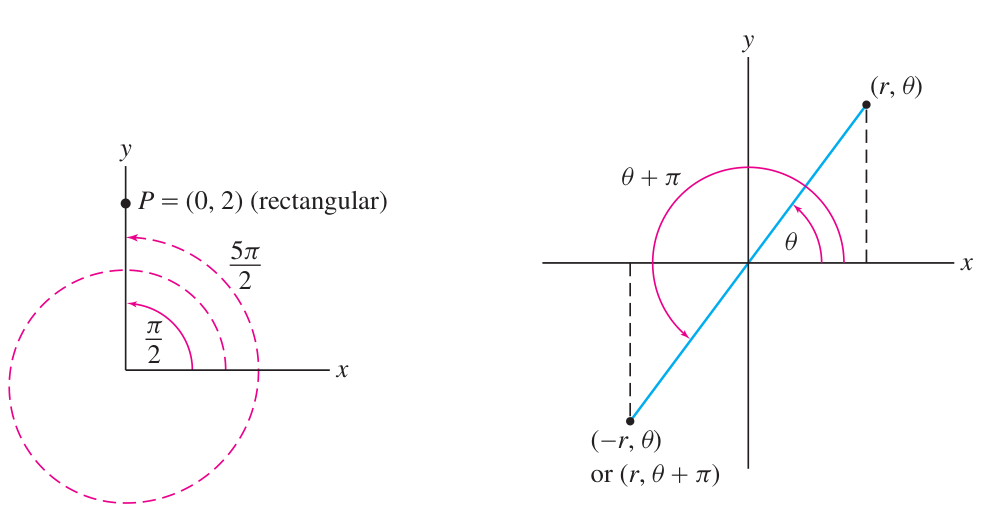
Polar coordinates have many redundancies: unlike Cartesian which are unique!

• For example:
  • And therefore also (negative can happen)
• For example: for every
• For example: for any

Polar coordinates cannot be added: they are not vector components!

• For example
• Whereas Cartesian coordinates can be added:

---

The transition formulas require careful choice of .

• The standard definition of sometimes gives wrong
  • This is because it uses the restricted domain ; the polar interpretation is: only points in Quadrant I and Quadrant IV (SAFE QUADRANTS)
• Therefore: check signs of and to see which quadrant, maybe need -correction!
  • Quadrant I or IV: polar angle is
  • polar angle is

---

Equations (as well as points) can also be converted to polar.

For , look for cancellation from .

For , try to keep inside of trig functions.

• For example:

Theory 2

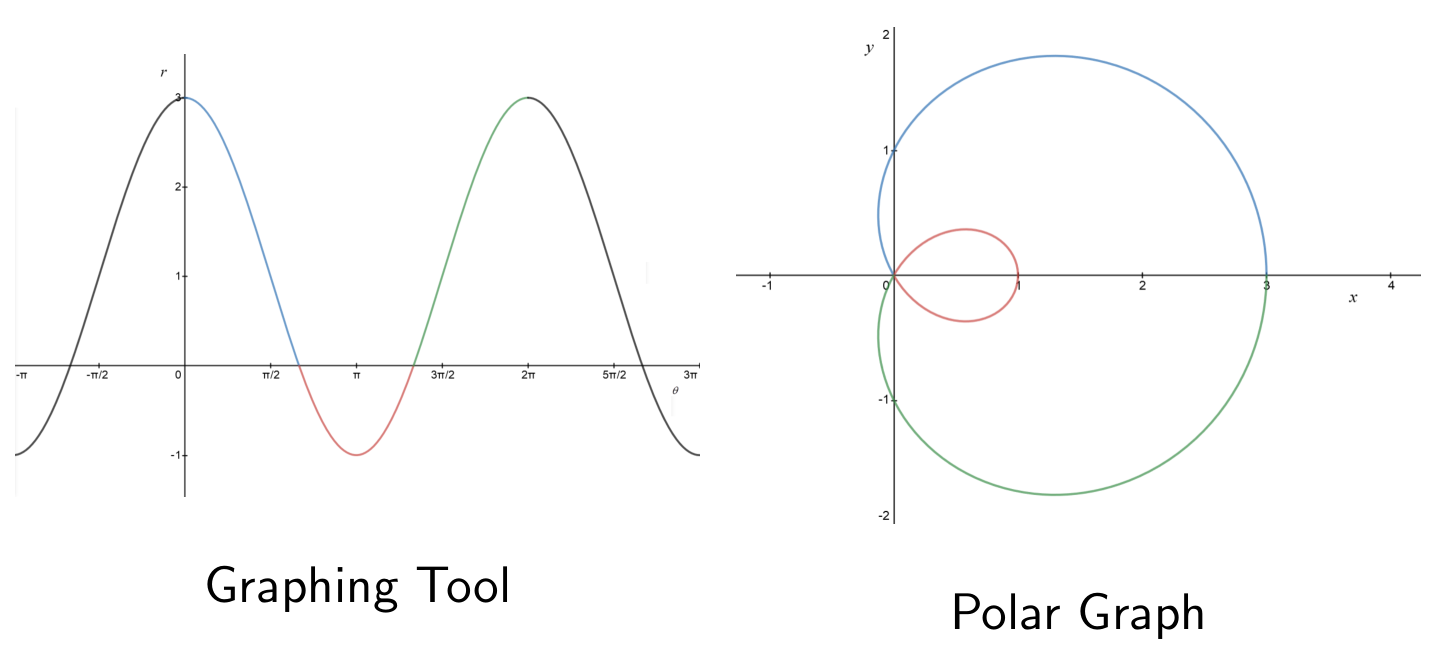
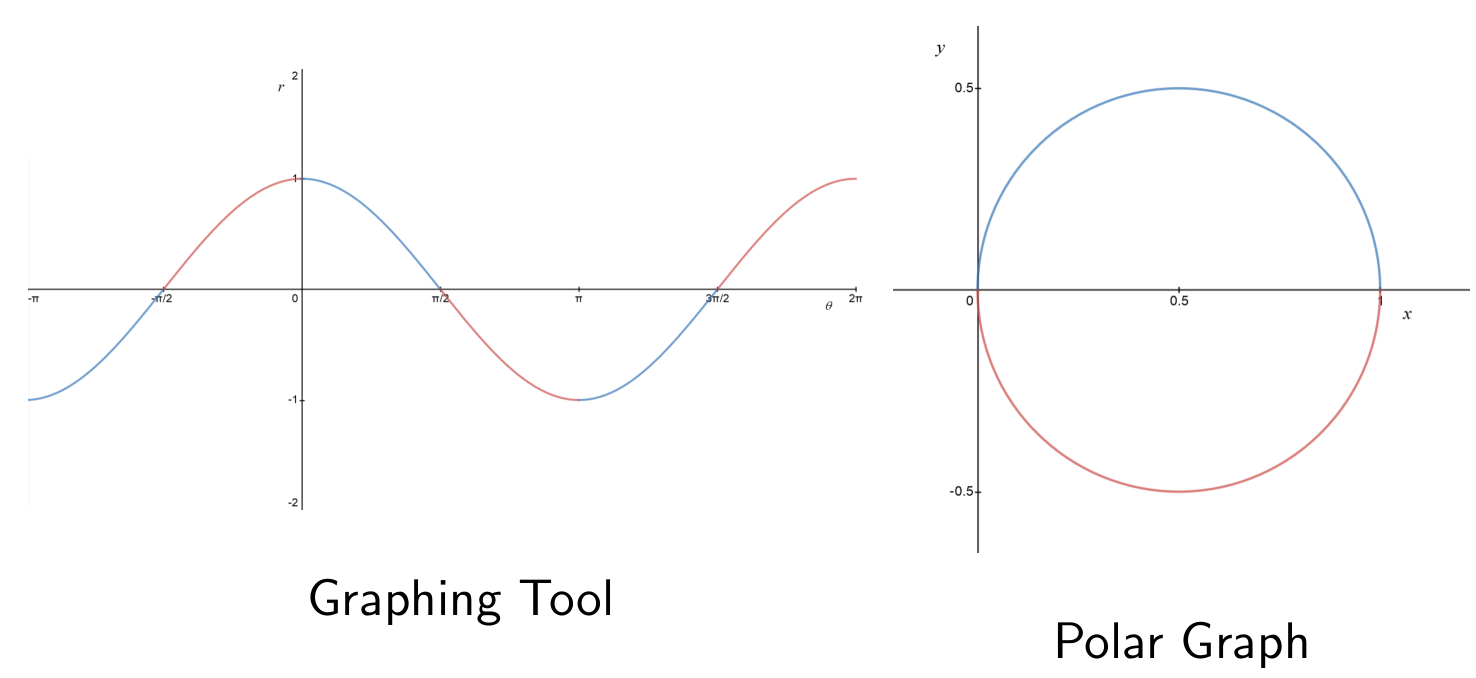
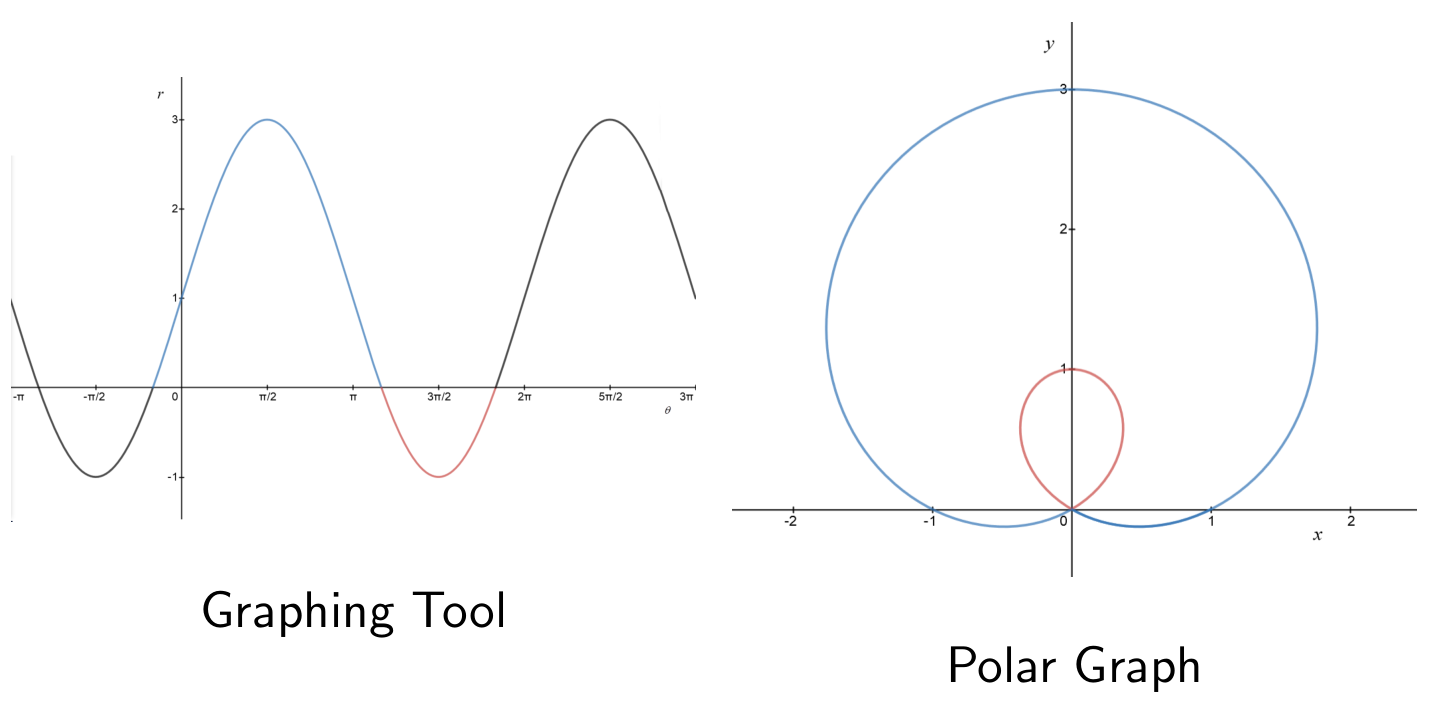
To draw the polar graph of some function, it can help to first draw the Cartesian graph of the function. (In other words, set and , and draw the usual graph.) By tracing through the points on the Cartesian graph, one can visualize the trajectory of the polar graph.

This Cartesian graph may be called a graphing tool for the polar graph.

---

A limaçon is the polar graph of .

The shape of a limaçon is determined by the value of . Any limaçon can be rescaled to have this form:

: Limaçon satisfying : unit circle.

: Limaçon satisfying : ‘outer loop’ circle with ‘flat spot’, not quite a ‘dimple’:

: Limaçon satisfying : ‘cardioid’ ‘outer loop’ circle with ‘dimple’ that creates a cusp:

: Limaçon satisfying : ‘dimple’ pushes past cusp to create ‘inner loop’:

: Limaçon satisfying : ‘inner loop’ only, no outer loop exists:

: Limaçon satisfying : ‘inner loop’ and ‘outer loop’ and rotated :

---

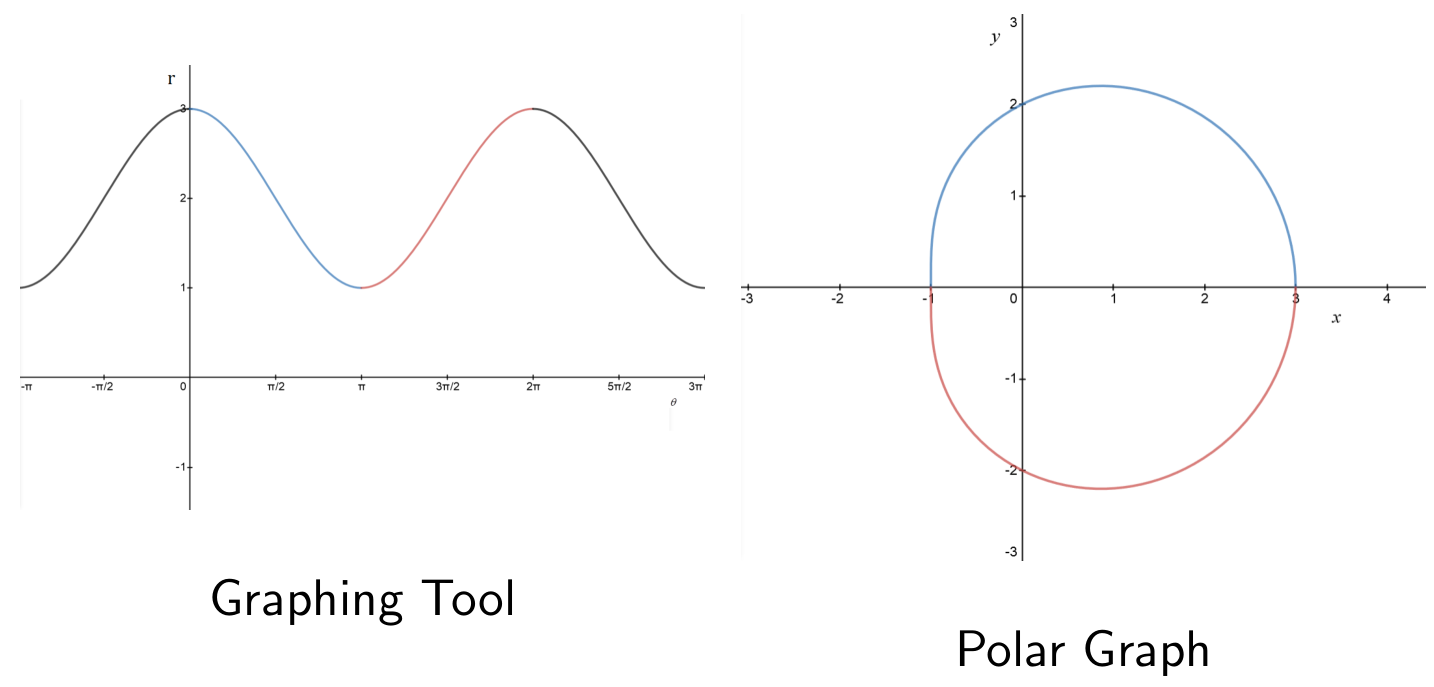
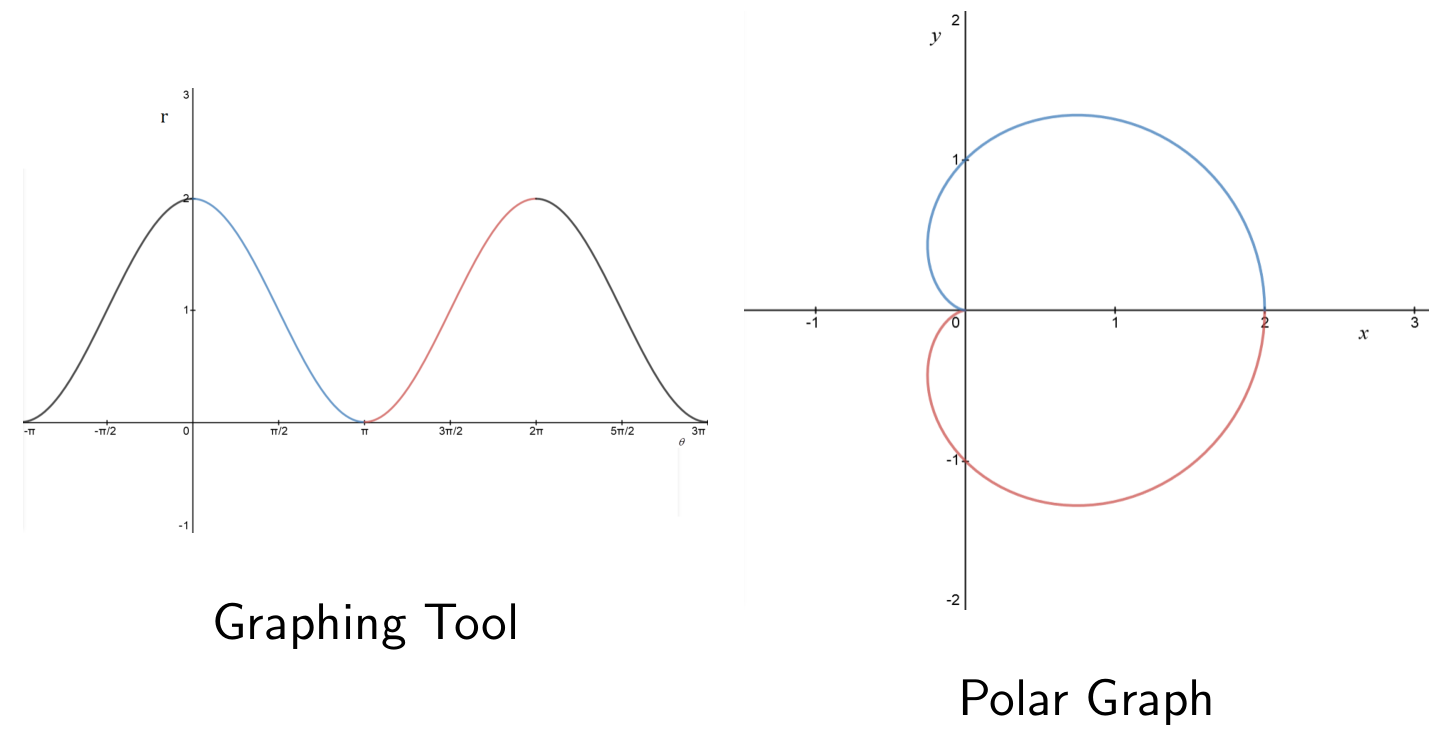
Transitions between limaçon types, :

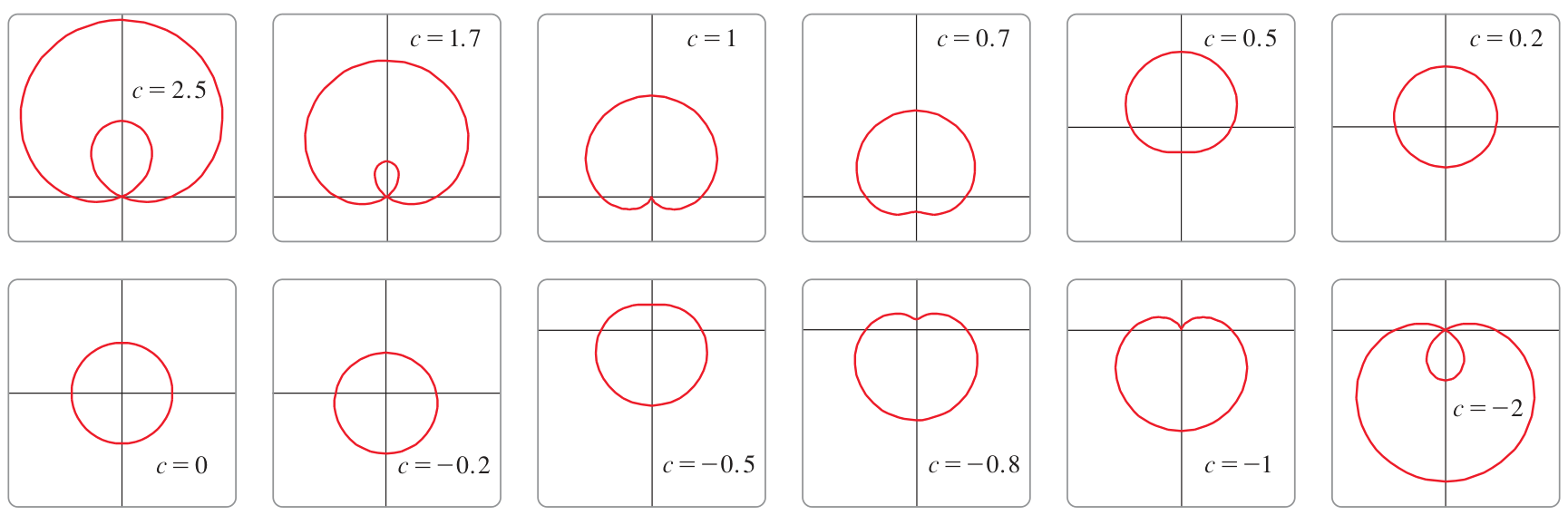
Notice the transition points at and :

The flat spot occurs when

• Smaller gives convex shape

The cusp occurs when

• Smaller gives dimple (assuming )
• Larger gives inner loop

Theory 3

Roses are polar graphs of this form:

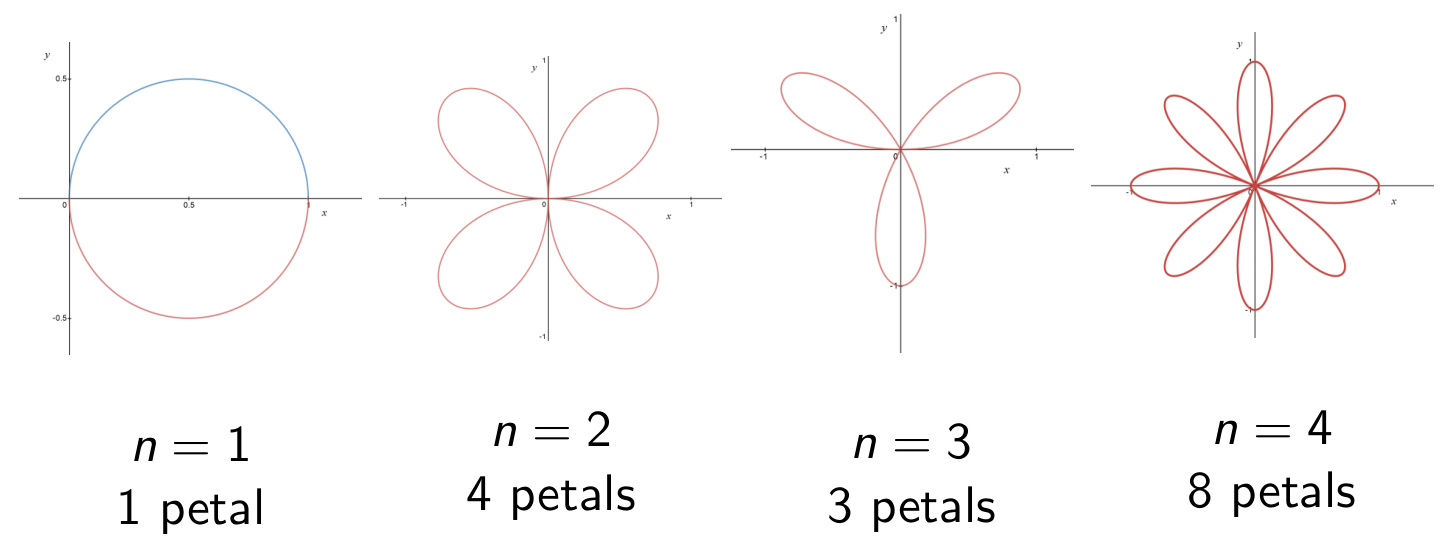
The pattern of petals:

• (even): obtain petals
  • These petals traversed once
• (odd): obtain petals
  • These petals traversed twice
• Either way: total-petal-traversals: always