Examples

Finding vertical tangents to a limaçon

Let us find the vertical tangents to the limaçon (the cardioid) given by .

Solution

(1) Convert to Cartesian parametric using and :

---

(2) Compute and :

---

(3) The vertical tangents occur when . We must double check that at these points.

Substitute and observe quadratic:

Solve:

Then find :

---

(4) Compute the points. In polar coordinates:

In Cartesian coordinates:

At :

At :

At :

---

(5) Correction: is a cusp!

The point at is on the cardioid, but the curve is not smooth there, this is a cusp.

Still, the left- and right-sided tangents exists and are equal, so in a certain sense we could say the curve has vertical tangent at .

Length of the inner loop

Consider the limaçon given by .

How long is the inner loop? Set up an integral for this quantity.

Solution

The inner loop is traced by the moving point when . This can be seen from the graph:

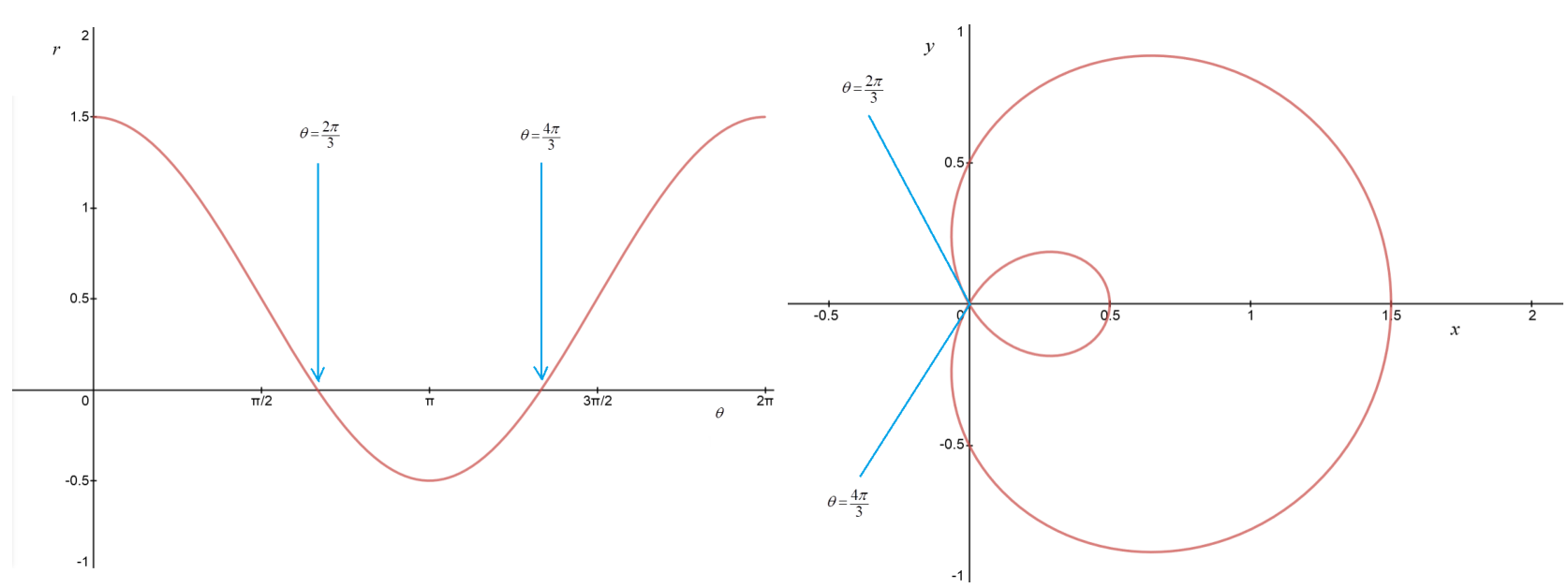
Therefore the length of the inner loop is given by this integral:

Area between circle and limaçon

Find the area of the region enclosed between the circle and the limaçon .

Solution

First draw the region:

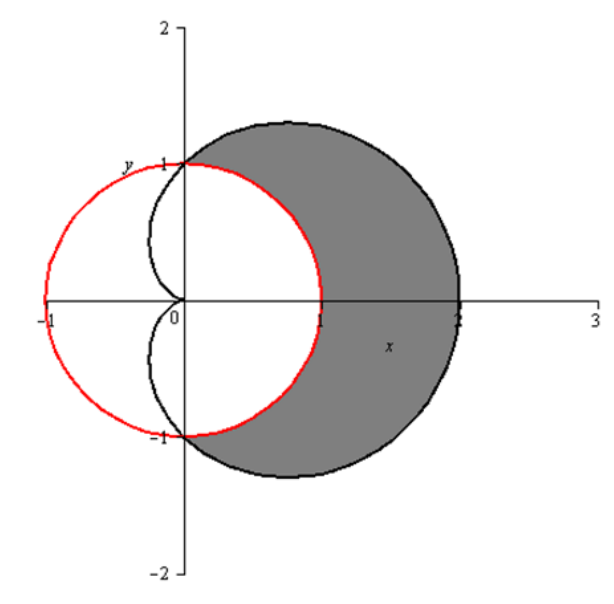
The two curves intersect at . Therefore the area enclosed is given by integrating over :

Area of small loops

Consider the following polar graph of :

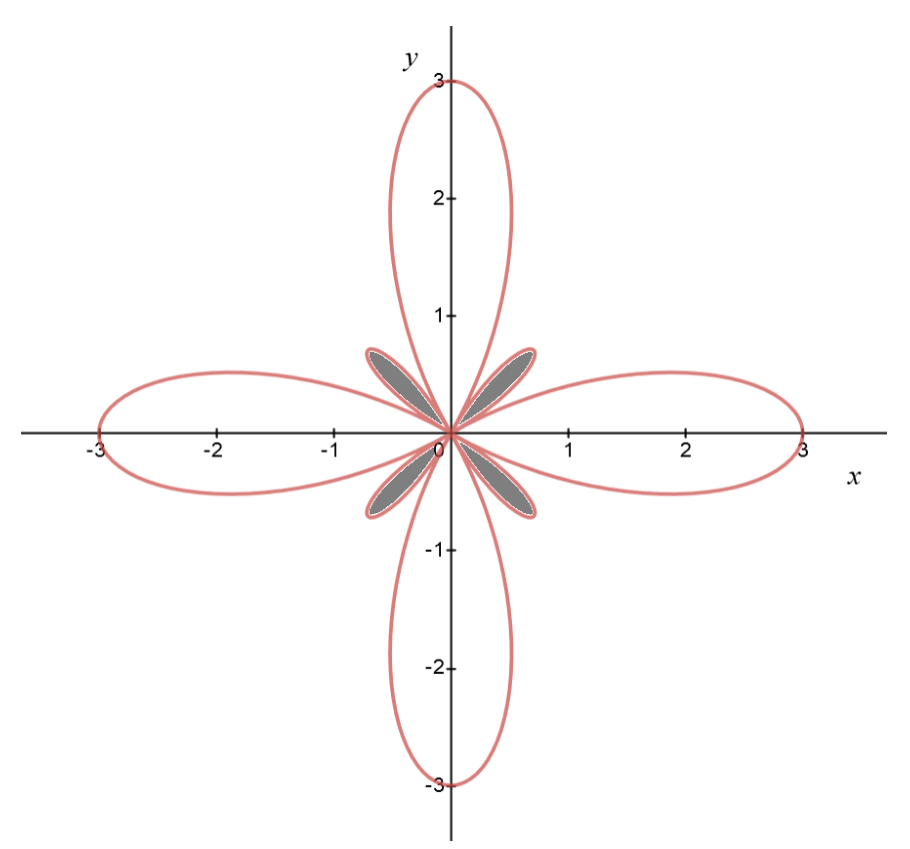
Find the area of the shaded region.

Solution

Find bounds for one small loop. Lower left loop occurs first. This loop is when .

Now set up area integral:

Power-to-frequency conversion: with :

Overlap area of circles

Compute the area of the overlap between crossing circles. For concreteness, suppose one of the circles is given by and the other is given by .

Solution

Drawing of the overlap:

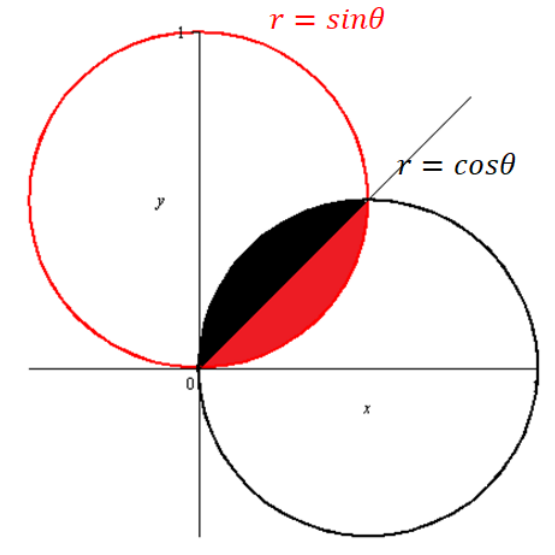
Notice: total overlap area = area of red region. Bounds for red region: .

Area formula applied to :

Power-to-frequency: :