01
Polar curve - Vertical or horizontal tangent lines
Find all points on the given curve where the tangent line is horizontal or vertical.
Hint: First determine parametric Cartesian coordinate functions using
as the parameter.
02
Arclength of one loop of a rose
Consider the graph of the polar curve
. Set up an integral which computes the arclength of one loop of this curve.
03
Polar curve - Slope of tangent line
Find the slope of the tangent line to the given polar curve:
Hint: First determine parametric Cartesian coordinate functions using
as the parameter.
04
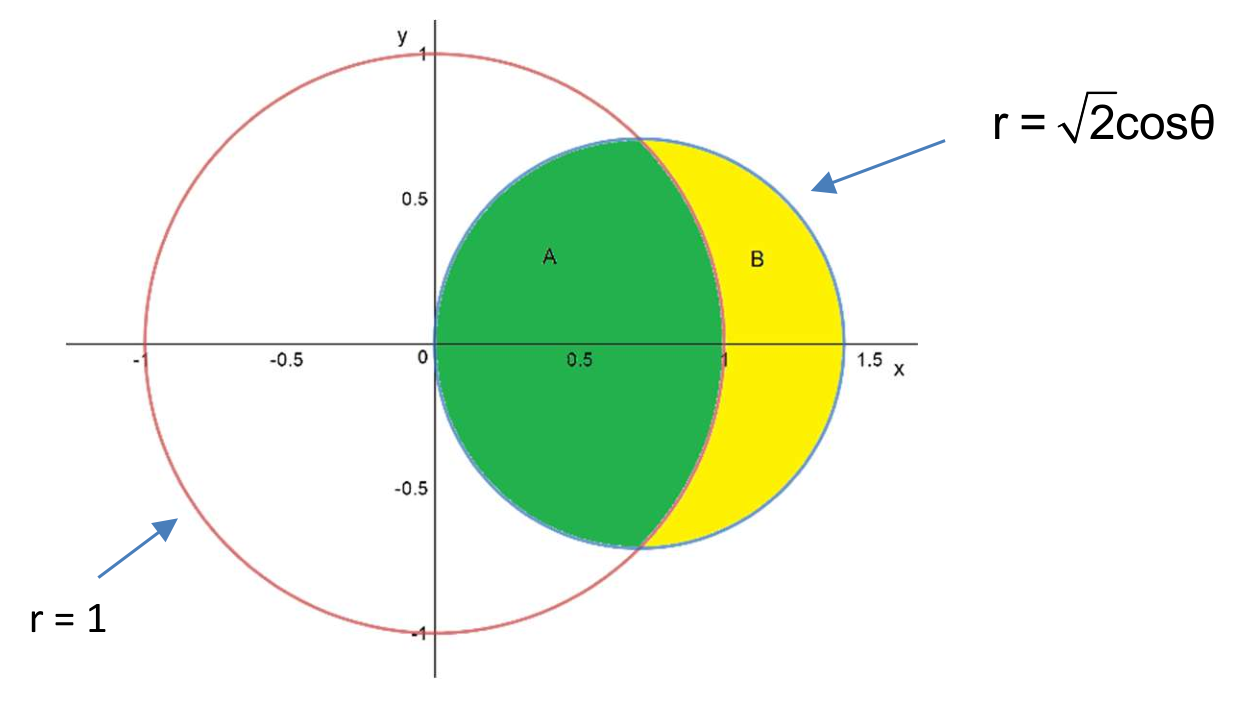
Polar coordinates - lunar areas
(a) Find the area of the green region.
(b) Find the area of the yellow region.
(You can find these in either order.)
05
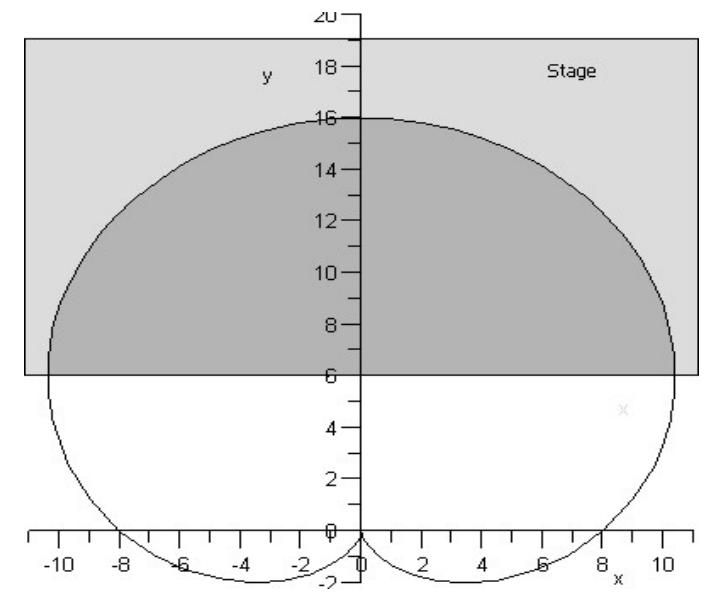
Pickup region of a microphone - limaçon area
The pickup region of a microphone is described by a limaçon with equation
, and part of the region is on a stage. Find the area of the part of the region on the stage.
06
Area of an inner loop
A limaçon is given as the graph of the polar curve
. Find the area of the inner loop of this limaçon.