Theory

Theory 1

A tree diagram depicts the components of a multi-stage experiment. Nodes, or branch points, represent sources of randomness.

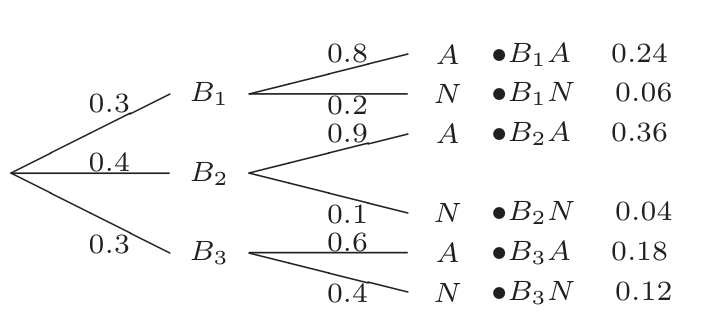
An outcome of the experiment is represented by a pathway taken from the root (left-most node) to a leaf (right-most node). The branch chosen at a given node junction represents the outcome of the “sub-experiment” constituting that branch point. So a pathway encodes the outcomes of all sub-experiments.

Each branch from a node is labeled with a probability number. This is the probability that the sub-experiment of that node has the outcome of that branch.

• The probability label on some branch is the conditional probability of that branch, assuming the pathway from root to prior node.
  • In the example: .
  • Therefore, branch labels from given node sum to 1. (Law of Total Probability)
• The probability of a given (overall) outcome is the product of the probabilities on each branch of the pathway to that outcome.
  • Makes sense, because (e.g.):
  • More generally: remember that (e.g.):
  • This overall outcome probability may be written at the leaf.

One can also use a tree diagram to remember quickly how to calculate certain probabilities.

For example, what is in the diagram? Answer: add up the pathway probabilities (leaf numbers) terminating in . That makes

For example, what is ? Answer: divide the leaf probability of by the total probability of . That makes: