01
Reliability for complex process
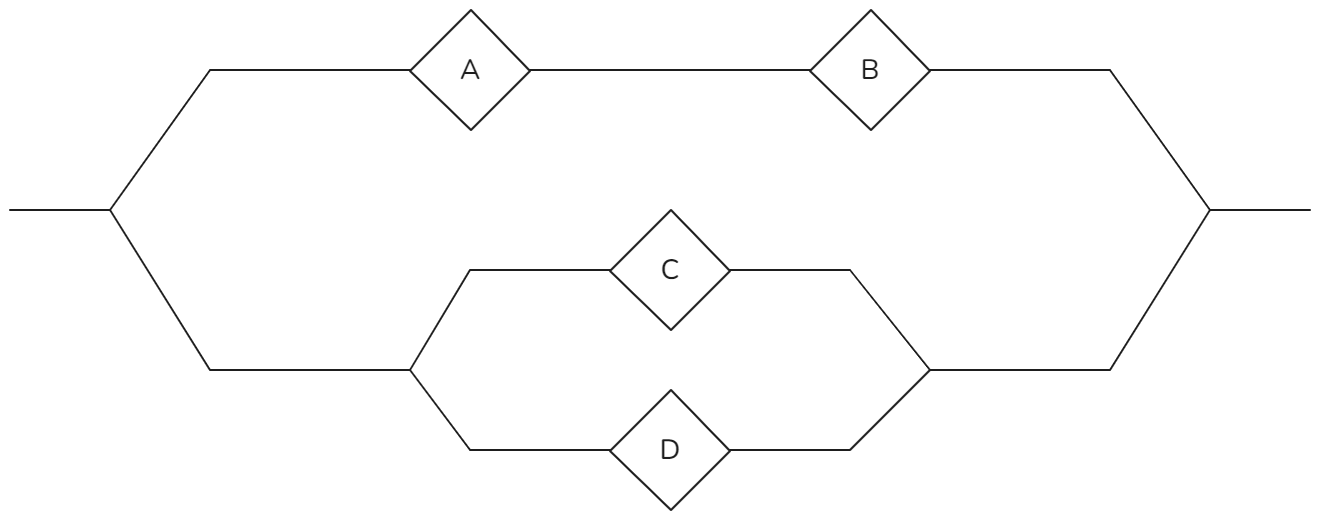
Consider a process with the following diagram of components in series and parallel:
Use
to denote the event that component succeeds. Suppose the success probabilities per component are given by this chart:
1 2 3 4 5 6 7 8 80% 60% 40% 90% 80% 50% 70% 90% What are the odds of success for the whole process?
Solution
09
(1) Describe dependencies of components.
The series 4, 5 runs parallel to component 3.
The components 2, 3, 4, 5, 6 all run in a series.
The latter is parallel to component 7
The circuit starts at component 1 and ends at component 8
(2) Find the probability the component 4 and 5 succeeded. (Denote as
)
(3) Find the probability 3, and
succeed. Note that these are in parallel. (Denote as )
(4) Find the probability 2,
, and 6 succeed. (Denote as )
(5) Find the probability 7 and
succeed. Note that these are in parallel. (Denote as )
(6) Lastly, find the probability
, , and 8 succeed. (Denote as ). Link to original
02
Enough staff to open
A small restaurant needs a minimum number of staff to open: 1 manager, 1 cook, 3 servers, and 1 host. Suppose there are 2 managers, 3 cooks, 3 servers, and 1 host. Each staff member is available with probability 0.95, and their availability is independent of others. What is the probability that the restaurant will have enough staff to open?
Solution
03
Reliability of a system
Consider the following system with components that are independent of each other. The probability that each individual component works are as follows:
, , , and .
What is the probability that the system works?
Solution
04
Reliability - Math competition cutoff score
At a high school math competition, students take a test with 10 questions. Each question is worth one point and the probability of a student getting any one question correct is 0.55, independent of the other questions.
(a) Find the probability of a student getting a score of 8 or higher.
(b) Students take the test individually but compete in teams of 2. To proceed to the second round of competition, each student on the team must score at least 8. Each high school can enter 2 teams. If a high school enters two teams, find the probability at least one of their teams will make it to the second round. Assume students’ scores are independent.
Solution
16
(a)
(b)
Link to original
05
Components of a car
A certain car includes
components, and it needs at least half of its components to function in order to drive. Each component functions with probability , independently of the others. For what values of
is a car with more likely to drive than a car with ? Start by defining a random variable that measures the number of functioning components.