Examples

PDF and CDF: Roll 2 dice

Roll two dice colored red and green. Let record the number of dots showing on the red die, the number on the green die, and let be a random variable giving the total number of dots showing after the roll, namely .

• Find the PMFs of and of and of .
• Find the CDF of .
• Find .

Solution

(1) Sample space.

Denote outcomes with ordered pairs of numbers , where is the number showing on the red die and is the number on the green one.

Require that are integers satisfying .

Events are sets of distinct such pairs.

---

(2) Create chart of outcomes.

Chart:

---

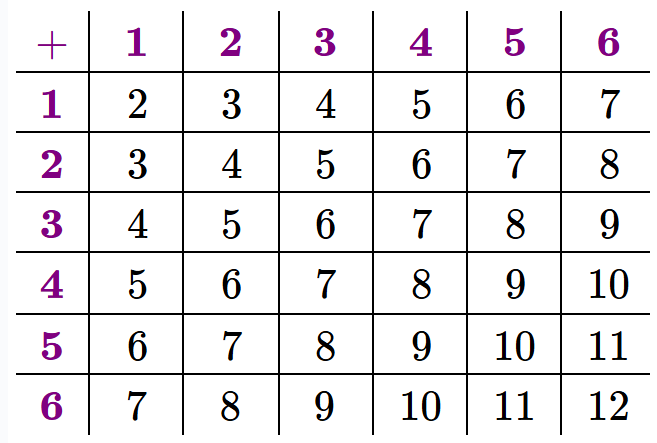
(3) Definitions of , , and .

We have and .

Therefore .

---

(4) Find PMF of .

Use variable for each possible value of , so .

Find :

Therefore for every .

---

(5) Find PMF of .

Same as for :

---

(6) Find PMF of .

Find :

Count outcomes along diagonal lines in the chart.

Create table of :

Create bar chart of :

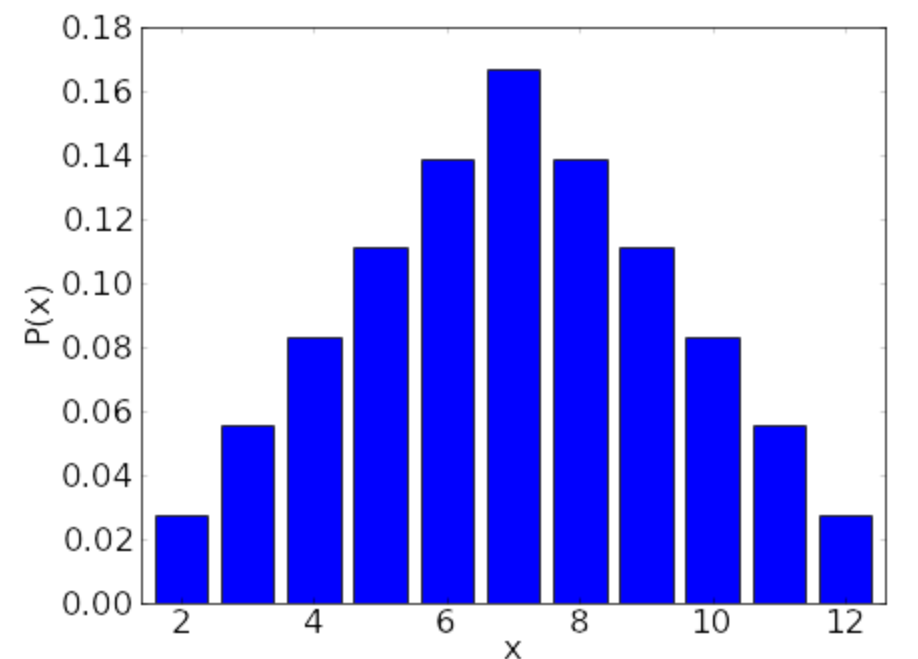
Evaluate: .

---

(7) Find CDF of .

CDF definition:

Apply definition: add new PMF value at each increment:

PMF for total heads count; binomial expansion of 1

A fair coin is flipped times.

Let be the random variable that counts the total number of heads in each sequence.

The PMF of is given by:

Since the total probability must add to 1, we know this formula must hold:

Is this equation really true?

There is another way to view this equation: it is the binomial expansion where and :

Life insurance payouts

A life insurance company has two clients, and , each with a policy that pays $100,000 upon death. Consider events that the older client dies next year, and that the younger dies next year. Suppose and .

Define a random variable measuring the total money paid out next year in units of $1,000. The possible values for are 0, 100, 200. We calculate: