Theory

Theory 1

Random variable

A random variable (RV) on a probability space is a function .

So assigns to each outcome a number.

Note: The word ‘variable’ indicates that an RV outputs numbers.

Random variables can be formed from other random variables using mathematical operations on the output numbers.

Given random variables and , we can form these new ones:

Suppose is some particular outcome. Then, for example, is by definition .

---

Random variables determine events.

• Given , the event “” is equal to the set
• That is: the set of outcomes mapped to by
• That is: the event “ took the value ”

Such events have probabilities. We write them like this:

This generalized to events where lies in some range or set, for example:

---

The axioms of probability translate into rules for these events.

For example, additivity leads to:

---

A discrete random variable has probability concentrated at a discrete set of real numbers.

• A ‘discrete set’ means finite or countably infinite.
• The distribution of probability is recorded using a probability mass function (PMF) that assigns probabilities to each of the discrete real numbers.
• Numbers with nonzero probability are called possible values.

PMF

The PMF function , for a discrete RV, is defined by:

A continuous random variable has probability spread out over the space of real numbers.

• The distribution of probability is recorded using a probability density function (PDF) which is integrated over intervals to determine probabilities.

PDF

The PDF function for (a CRV) is written for , and probabilities are calculated like this:

---

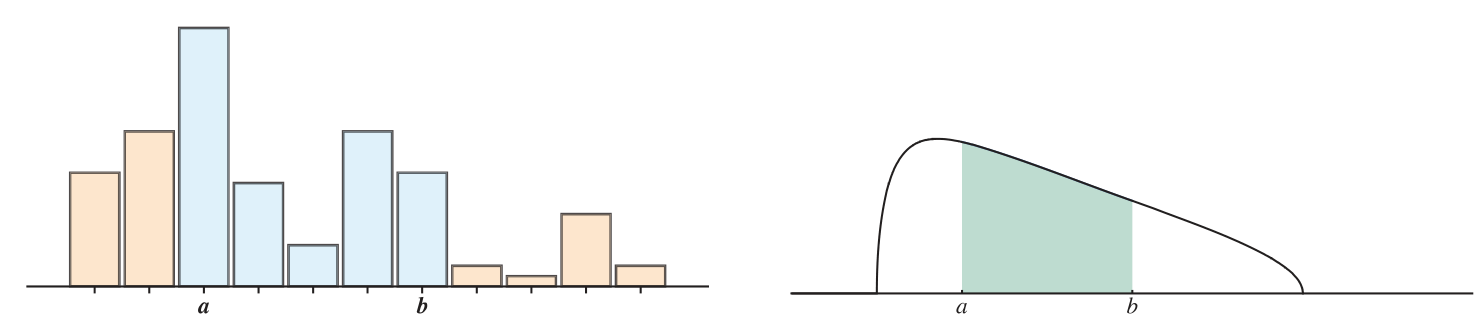
For any RV, whether discrete or continuous, the distribution of probability is encoded by a function:

CDF

The cumulative distribution function (CDF) for a random variable is defined for all by:

Notes:

• Sometimes the relation to is omitted and one sees just “.”
• Sometimes the CDF is called, simply, “the distribution function” because:

The CDF works for a discrete, continuous, or mixed RV

• PMF is for discrete only
• PDF is for continuous only
• CDF covers both and covers mixed RVs

---

The CDF of a discrete RV is always a stepwise increasing function. At each step up, the jump size matches the PMF value there.

From this graph of :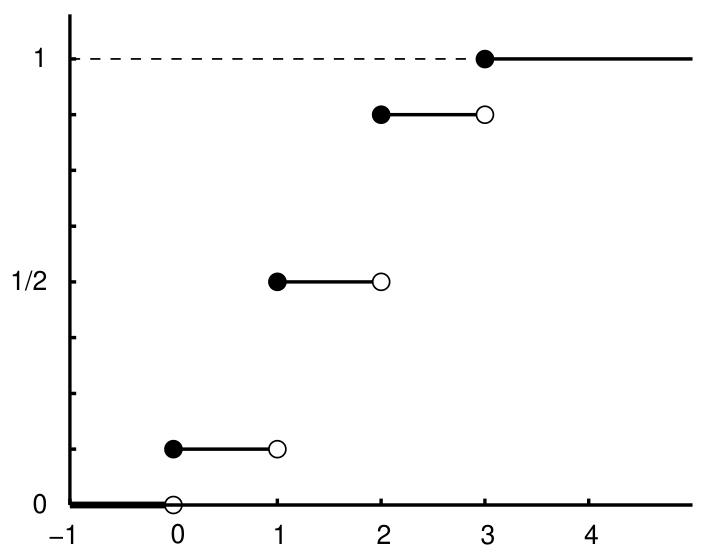

we can infer the PMF values based on the jump sizes:

---

For a discrete RV, the CDF and the PMF can be calculated from each other using formulas.

PMF from CDF from PMF

Given a PMF , the CDF is determined by:

where is the set of possible values of .

Given a CDF , the PMF is determined by: