02
PMF and CDF: number of heads in five flips
Let
count the number of heads resulting from five flips of a coin. Write complete formulas (using cases) for the PMF and CDF of
.
Solution
02
(1) Identify distribution.
We have that
, since there are trials and .
(2) Use binomial distribution formula to get PMF.
(3) Find CDF.
Since
, we have
(4) Write out explicit values of CDF.
Link to original
03
Rolling until a six
A fair die is rolled until a six comes up.
What are the odds that it takes at least 10 rolls? (Use a geometric random variable.)
Solution
13
(1) Define random variables.
Let
. We wish to find
. For all
, , the first trials result in failure, and the trial is a success.
(2) Compute probability.
Note that the summation is simplified using the formula for a geometric series.
Link to original
04
Intersection accidents
Suppose that the odds of an accident occurring on any given day at the intersection of Ivy and Emmet is 0.05.
What are the odds of the first accident occurring between day 5 and day 10, inclusive? (Use an appropriate discrete distribution type.)
Solution
04
(1) Define random variables.
Let
. We wish to find
.
(2) Compute
using the formula for a geometric distribution. Link to original
05
A very strange car
A very strange car with
components will drive if at least half of its components work. Each component will work with the same probability , independently of the others. For what values of
is a car with more likely to drive than a car with ? (Start by defining a random variable that counts the number of working components.)
Solution
05
(1) Define random variables.
Let
represent the car with three components. Let
represent the car with five components.
(2) Find probabilities that both cars work.
For the three-component car, we want
, so For the five-component car, we want
, so
(3) Find when
. Solve the inequality for
. Link to original
06
Geometric distribution is memoryless
Suppose that
. Derive this equation:
Interpret the equation. (Inspired by the title.)
Solution
06
(1) Set up conditional probability formula.
(2) Find formulas for numerator and denominator.
(3) Plug in values into initial formula
Link to original
07
Binomial ratios
Suppose
.
- Find the value of
that maximizes . Do this by studying the successive ratios . - Use these ratios to compute
as a sum of 5 terms without using factorials. Do this by computing directly, and then writing a recursive algorithm that determines in terms of .
Solution
07
(1) Find formula for ratio
.
(2) Interpret ratio.
We want
, so . Solving for
, we get . Since
is an integer, the is maximized when .
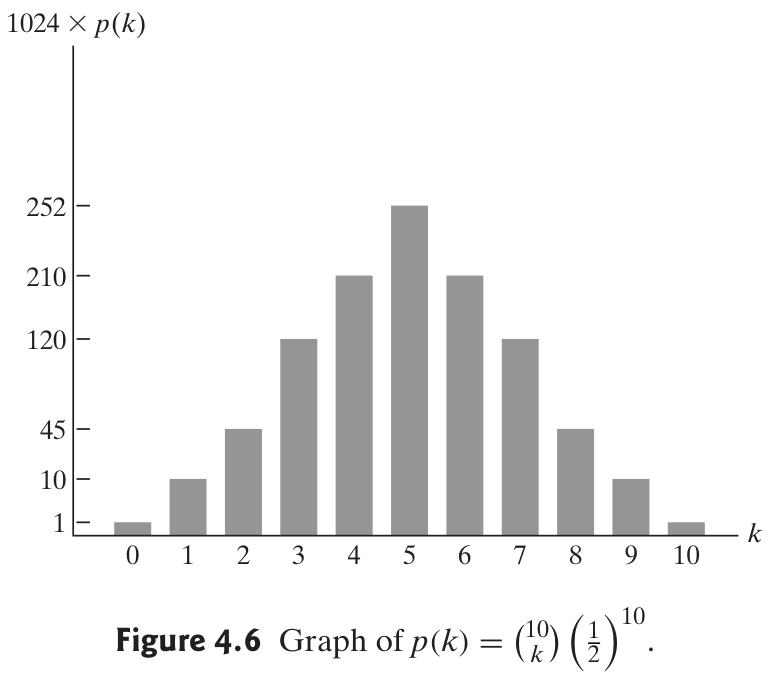
(3) Compute
directly. Based on the figure,
and .
(4) Use ratio to solve for successive terms.
(5) Add up probabilities.
Link to original
08
Prize on the Mall
A booth on the Mall is running a secret prize game, in which the
passerby wearing a hat wins $1,000. Passersby wear hats independently of each other and with probability 20%.
Let
be a random variable counting how many passersby pass by before a winner is found. (a) What is the name of the distribution for
? What are the parameters? (b) What is the probability that the
passerby wins the prize? (c) What is the probability that at least
passersby are needed before a winner is found?
Solution
08
(a)
Identify the distribution.
follows a negative binomial distribution with parameters and .
(b)
Compute
.
(c)
Compute
. We know that the minimum number of passersby before a winner is declared is
. Therefore,
. Link to original
09
Lottery game
Suppose a lottery game requires that you purchase a $10 game card and advertises a 10% probability of winning a prize.
If you keep purchasing these game cards until you win twice, what is the probability you will purchase at least 4 of them?
Solution