Examples

Sum of parabolic random variables

Suppose is an RV with PDF given by:

Let be an independent copy of . So , but is independent of .

Find the PDF of .

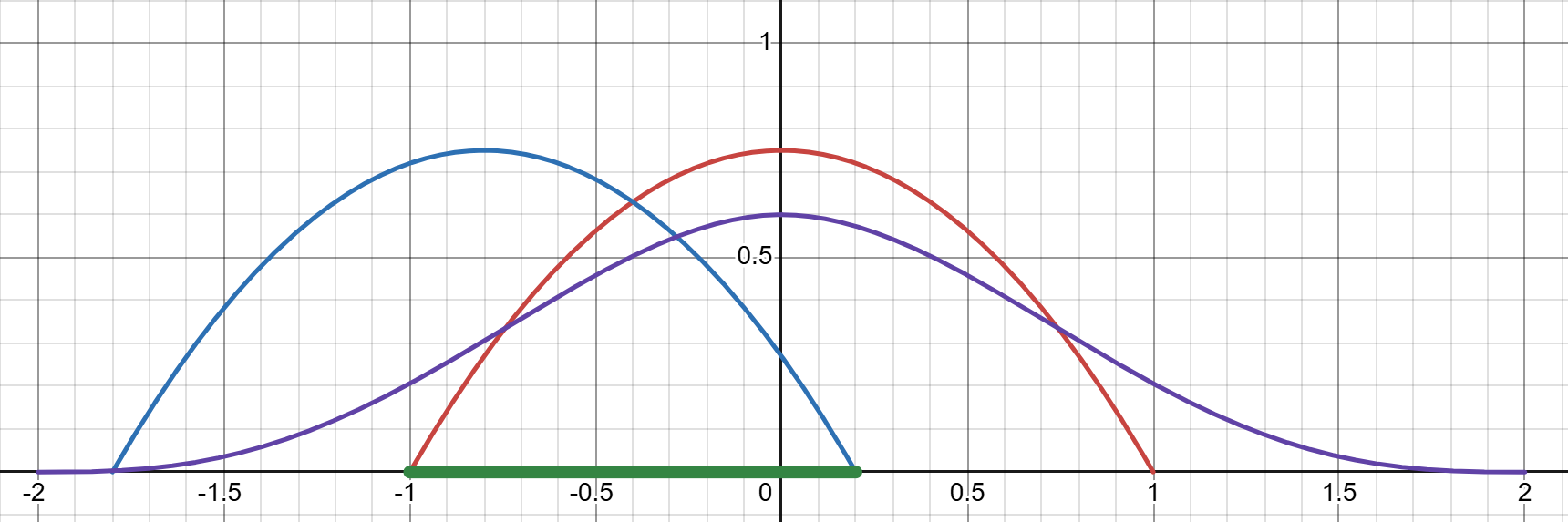
Solution

The graph of matches the graph of except (i) flipped in a vertical mirror, (ii) shifted by to the left.

When , the integrand is nonzero only for :

When , the integrand is nonzero only for :

Final result is:

Discrete PMF formula for a sum

Verify the discrete formula for the PMF of a sum. (Apply the general formula for the PMF of .)

Vandermonde’s identity from the binomial sum rule

Show that this “Vandermonde identity” holds for positive integers :

Hint: The binomial sum rule is:

Set . Compute the PMF of the left side using convolution. Compute the PMF of the right side directly. Set these PMFs equal.

Convolution practice

Suppose is an RV with density:

Suppose is uniform on and independent of .

Find the PDF of . Sketch the graph of this PDF.

Exp plus Exp equals Erlang

Let us verify this formula by direct calculation:

Solution

Let be independent RVs.

Therefore:

Now compute the convolution, assuming :

This is the Erlang PDF:

Combining normals

Suppose , . Find the probability that .

Solution

Define . Using the formulas above, we see , or for a standard normal . Then: