Theory

Theory 1 - Minimum mean square error

Suppose our problem is to estimate or guess or predict the value of a random variable in a particular run of our experiment. Assume we have the distribution of . Which value do we choose as our guess?

There is no single best answer to this question. The “best guess” number depends on additional factors in the problem context.

One method is to pick a value where the PMF or PDF of is maximal. This is a value of highest probability. There may be more than one!

Another method is to pick the expected value . This value may be impossible!

For the normal distribution, or any symmetrical distribution, these are the same value. For most distributions, though, they are not the same.

---

Mean square error (MSE)

Given some estimate for a random variable , the mean square error (MSE) of is:

The MSE quantifies the typical (square of the) error. Error here means the difference between the true value and the estimate .

Other error estimates are reasonable and useful in niche contexts. For example, or . They are not frequently used, so we do not consider their theory further.

---

In problem contexts where large errors are more costly than small errors (i.e. many real problems), the most likely value of (the point with maximal PDF) may fare poorly as an estimate.

It turns out that the expected value also happens to be the value that minimizes the MSE.

Expected value minimizes MSE

Given a random variable , its expected value is the estimate of with minimal mean square error.

The MSE error for is:

Proof that minimizes MSE

Expand the MSE error:

Now minimize this parabola. Differentiate:

Find zeros:

---

When the estimate is made in the absence of information (besides the distribution of ), it is called a blind estimate. Therefore, is the blind minimal MSE estimate, and is the error of this estimate.

In the presence of additional information, for example that event is known, then the MSE estimate is and the error of this estimate is .

The MSE estimate can also be conditioned on another variable, say :

Minimal MSE of given

The minimal MSE estimate of given another variable :

The error of this estimate is , which equals .

Notice that the minimal MSE of given can be used to define a random variable:

This is a derived variable from given by composing with the function .

The variable provides the minimal MSE estimates of when experimental outcomes are viewed as providing the information of only, and the model is used to derive estimates of from this information.

Theory 2 - Line of minimal MSE

Linear approximation is very common in applied math.

One could consider the linearization of (its tangent line at some point) instead of the exact function .

One could instead minimize the MSE over all linear functions of . (Each of which is an RV.) The line with minimal MSE is called the linear estimator.

The difference here is:

• line of best fit at a single point vs.
• line of best fit over the whole range of and —weighted by likelihoods

Linear estimator: Line of minimal MSE

Let be an arbitrary line . Let .

The mean square error (MSE) of this line is:

The linear estimator of in terms of is the line with minimal MSE, and it is:

The error value at the (best) linear estimator, , is:

Theorem: The error variable of the linear estimator, , is perfectly uncorrelated with .

Slope and

Notice:

Thus, for standardized variables and , it turns out is the slope of the linear estimator.

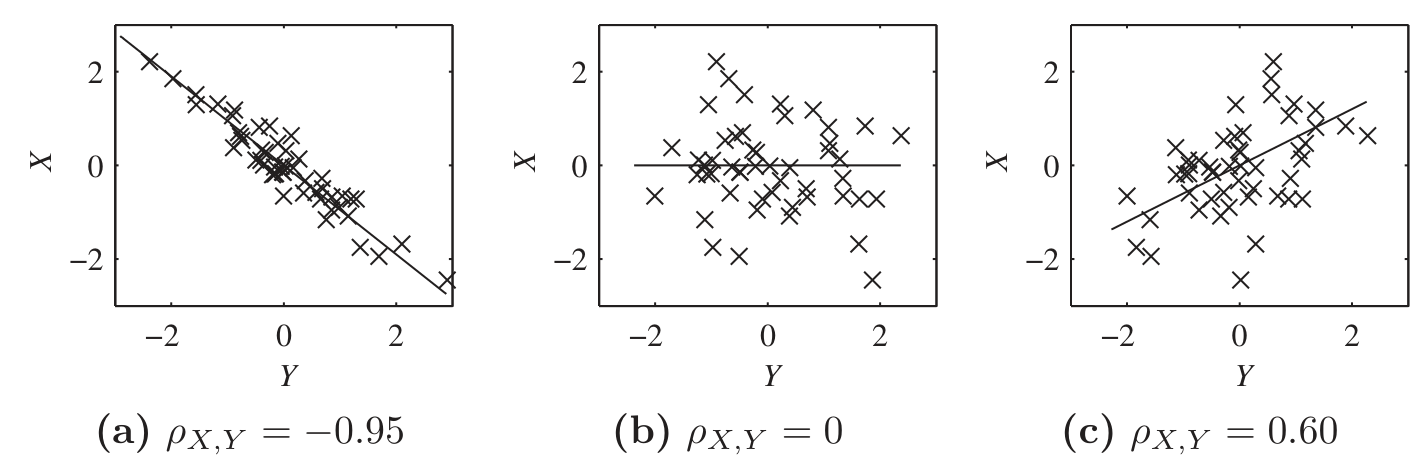
In each graph, and .

The line of minimal MSE is the “best fit” line, .