W03 - Examples

Repeated trials

19 - Multinomial: Soft drinks preferred

Folks coming to a party prefer Coke (55%), Pepsi (25%), or Dew (20%). If 20 people order drinks in sequence, what is the probability that exactly 12 have Coke and 5 have Pepsi and 3 have Dew?

Solution The multinomial coefficient gives the number of ways to assign 20 people into bins according to preferences matching the given numbers, and and .

Each such assignment is one sequence of outcomes. All such sequences have probability .

The answer is therefore:

Reliability

20 - Reliability: Series, parallel, series

Suppose a process has internal components arranged like this: 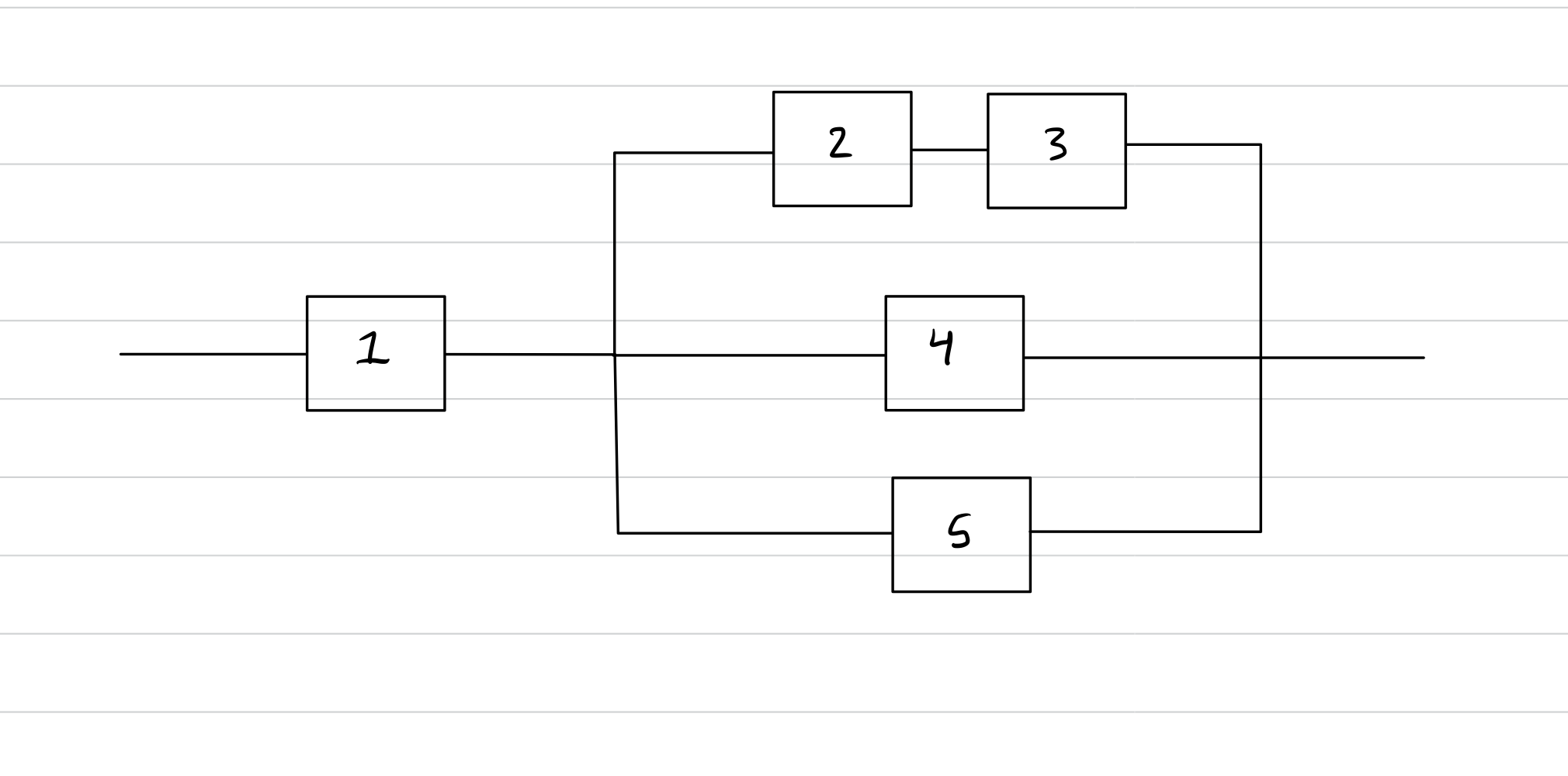Write for the event that component succeeds, and for the event that it fails.

The success probabilities for each component are given in the chart:

1	2	3	4	5
92%	89%	95%	86%	91%

Find the probability that the entire system succeeds.

Solution

• && Conjoin components 2 and 3 in series.
  • Compute:
  • Therefore:
• && Conjoin components (2-3) with 4 and 5 in parallel.
  • Compute for the complement (failure) first:
  • Flip back to success:
• & Conjoin components 1 with (2-3-4-5) in series.
  • Compute:

Discrete random variables

21 - PDF and CDF: Roll 2 dice

Roll two dice colored red and green. Let record the number of dots showing on the red die, the number on the green die, and let be a random variable giving the total number of dots showing after the roll, namely .

• Find the PMFs of and of and of .
• Find the CDF of .
• Find .

Solution

• & Sample space.
  • Denote outcomes with ordered pairs of numbers , where is the number showing on the red die and is the number on the green one.
  • Require that are integers satisfying .
  • Events are sets of distinct such pairs.
• && Create chart of outcomes.
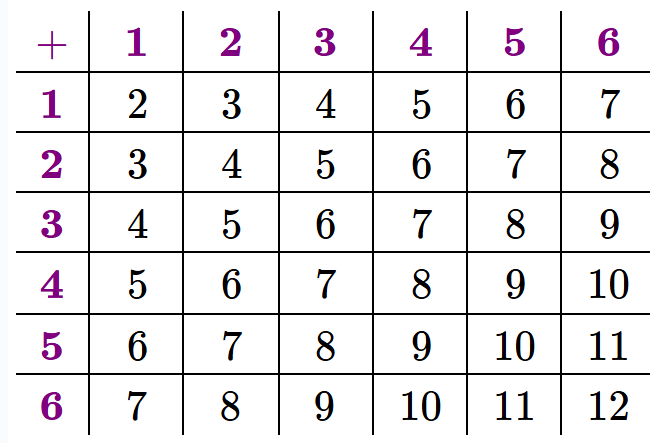
  • Chart:
• & Definitions of , , and .
  • We have and .
  • Therefore .
• && Find PMF of .
  • Use variable for each possible value of , so .
  • Find :
  • Therefore for every .
• & Find PMF of .
  • Same as for :
• &&& Find PMF of .
  • Find :
  • !! Count outcomes along diagonal lines in the chart.
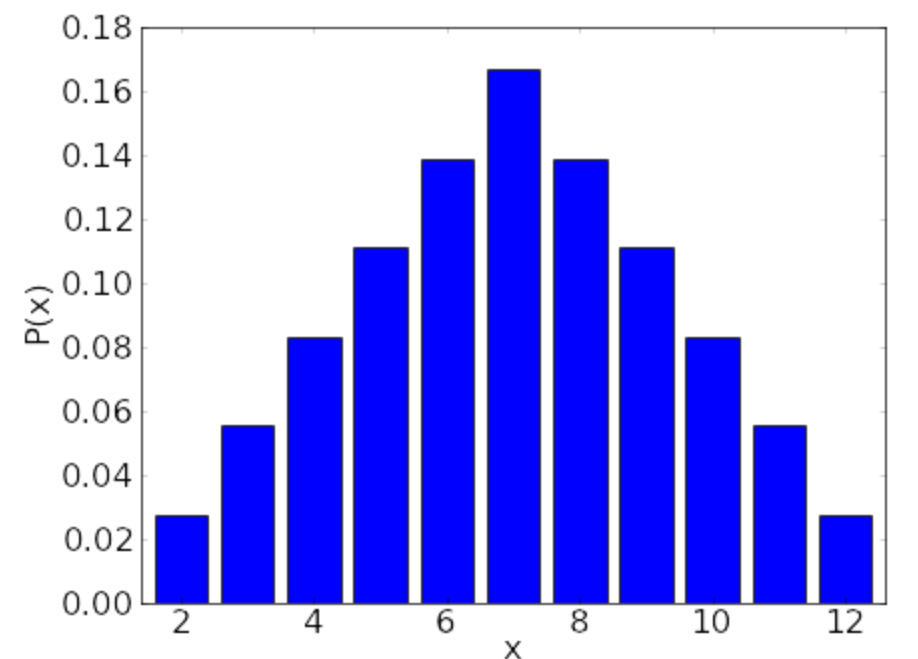
  • Create table of :
  • Create bar chart of :
  • Evaluate: .
• &&& Find CDF of .
  • CDF definition:
  • Apply definition: add new PMF value at each increment:

22 - PMF for total heads count; binomial expansion of 1

A fair coin is flipped times.

Let be the random variable that counts the total number of heads in each sequence.

The PMF of is given by: Since the total probability must add to 1, we know this formula must hold:

Is this equation really true?

There is another way to view this equation: it is the binomial expansion where and :

23 - Life insurance payouts

A life insurance company has two clients, and , each with a policy that pays $100,000 upon death. Consider events that the older client dies next year, and that the younger dies next year. Suppose and .

Define a random variable measuring the total money paid out next year in units of $1,000. The possible values for are 0, 100, 200. We calculate: