Counting
01
Rolling two dice
Two dice are rolled. Find the probabilities of the following events:
, the event that the sum is 10 , the event that the sum is 12 , the event that the two numbers are equal
02
Binomial - Repeated coin flips
A coin is flipped 7 times and the sequence of results recorded as an outcome.
(a) How many possible outcomes have exactly 3 heads?
(b) How many possible outcomes have at least 3 heads?
03
Multinomial - Colored marbles in a line
How many ways are there to line up 10 colored marbles (2 red, 3 white, 5 blue), assuming you cannot distinguish marbles of the same color?
04
Multinomial - Many rolls of a die
Roll a die 100 times.
(a) What is the probability that you rolled exactly 16 ones and 17 twos? (No need to simplify your answer.) Hint: use three bins. What are the bins?
(b) Using summation notation, write down a formula for the probability of rolling exactly 25 ones and at least 50 twos.
For this problem, use “desired outcomes over total outcomes” (simple counting), not repeated trials theory (next section).
Repeated trials
05
Independent trials - At least 45 good paper clips
For a paper clip production line, 90% of the paper clips come off good, and 10% come off broken.
You buy a box of 50 paper clips from this line. What is the probability that at least 45 of them are good?
06
Geometric wait time - Takes 10 rolls to get 6
A fair die is rolled until a six comes up. What are the odds that it takes at least 10 rolls?
Hint: you might find it easier to compute the odds of the complementary event.
07
Intersection accidents
Suppose that the odds of an accident occurring on any given day at the intersection of Ivy and Emmet is 0.05.
(a) What are the odds of a perfect week? (No accidents.)
(b) What are the odds of exactly 2 accidents in 30 days?
(c) What are the odds of the first accident occurring after day 4 and by day 10?
08
Guessing on a test
Your odds of getting any given exam question right are
. The exam has 4 questions, and you need to answer 3 correctly to pass. (a) What is the probability that you pass?
(b) After finishing the exam, you are 100% sure that you got the second question right. Now what are the odds that you pass?
Reliability
09
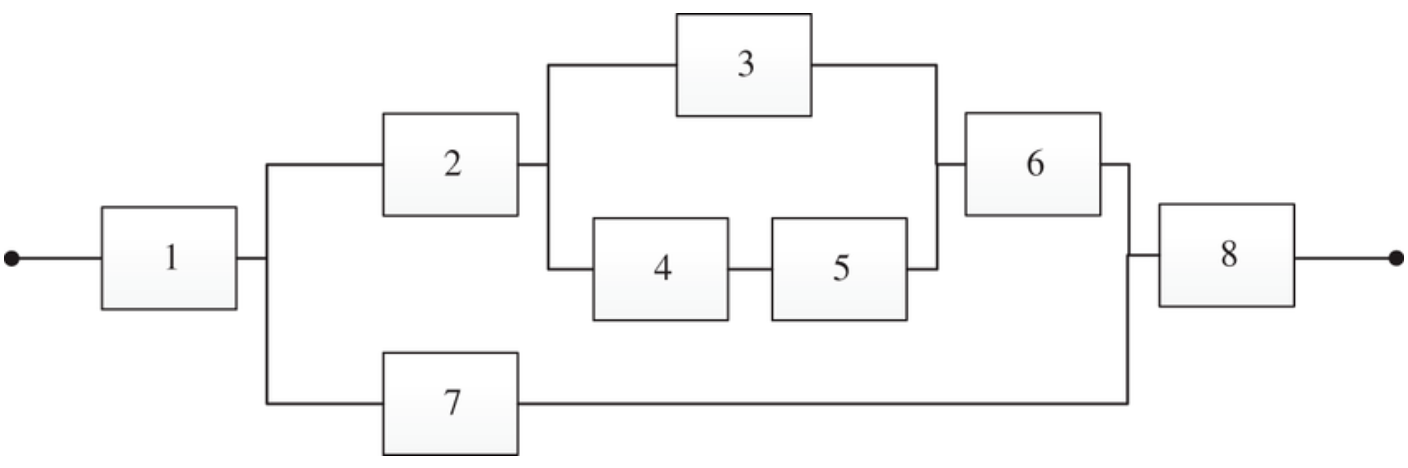
Reliability for complex process
Consider a process with the following diagram of components in series and parallel:
Use
to denote the event that component succeeds. Suppose the success probabilities per component are given by this chart:
1 2 3 4 5 6 7 8 80% 60% 40% 90% 80% 50% 70% 90% What are the odds of success for the whole process? ^u81sr3
Discrete random variables
10
Digit of a real number
Suppose a real number is chosen randomly in the unit interval
. Consider the decimal expansion of this number. Let be a random variable giving the first digit after the decimal point. Find the possible values, the PMF, and the CDF of .
11
Gambling with a coin
Two players, A and B, are flipping a fair coin together. If it comes up heads, A pays $1 to B, and if it comes up tails, B pays $1 to A.
They play five rounds. Let
be a random variable recording A’s final winnings. (a) Describe the set of possible values of
. (b) Describe the PMF and CDF of
.