Course Landing Page

W07 - Examples

5 min read

Joint distributions

Joint and marginal PMFs - Smaller and bigger roll

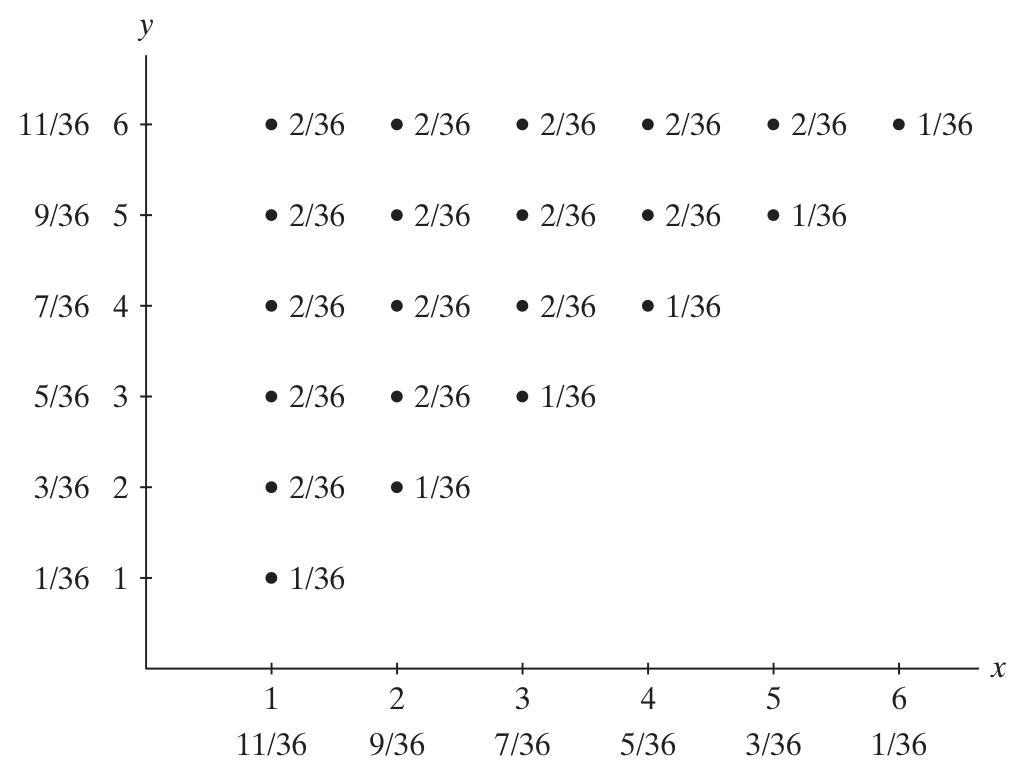
Roll two dice, and let indicate the smaller of the numbers rolled, and let indicate the bigger number.

Make a chart showing the PMF. Compute the marginal probabilities, and write them in the margins of the chart.

Solution

400

Event probability drawn from PMF table

Here is a joint PMF table:

Using the table, compute the following event probabilities: (a) (b) (c) (d)

Joint and marginal PMFs - Coin flipping

Flip a fair coin four times. Let measure the number of heads in the first two flips, and let measure the total number of heads.

Make a chart showing the PMF. Compute the marginal probabilities, and write them in the margins of the chart.

Marginal and event probability from joint density

Suppose the joint density of and is given by: Find and .

Solution Compute the marginal PDF:

Find probability of the event :

Marginals from joint density

The joint PDF for and is given by:

Find and .

Event probability from joint density

The joint PDF for and is given by: Compute .

Independent random variables

Event probability - Meeting in the park

A man and a woman arrange to meet in the park between 12:00 and 1:00 am. They both arrive at a random time with uniform distribution over that hour, and do not coordinate with each other.

Find the probability that the first person to arrive has to wait longer than 15 minutes for the second person to arrive.

Solution Let denote the time the man arrives. Use minutes starting from 12:00, so . Let denote the time the woman arrives, using the same interval.

The probability we seek is: Because and are symmetrical in probability, these terms have the same value, so we just double the first one for our answer.

Since the arrivals are independent of each other, we have .

Since each arrival time is uniform over the interval, we have: Therefore the joint density is . Calculate:

Uniform disk: Cartesian vs. polar

Suppose that a point is chosen uniformly at random on the unit disk.

(a) Let and be the Cartesian coordinates of the chosen point. Are and independent?

(b) Let and give the polar coordinates of the chosen point. Are and independent?

Solution (a) Write for the joint distribution of and . We have:

Then computing , we obtain:

By similar reasoning, for .

The product is not equal to , so and are not independent. Information about the value of does provide constraints on the possible values of , so this result makes sense.

(b) To find the marginals and , the standard method is to integrate the density in the opposite variables.

  • !! The probability density is not constant! The area of a differential sector depends on .

We can take two approaches to finding the density .

  • (i) Area of a differential sector divided by total area
    • So the density is
  • (ii) Compute CDF first, then use partial derivatives.

Elaborating on (ii): joint CDF then partials for joint PDF

The region ‘below’ a given point , in polar coordinates, is a sector with area . The factor is a percentage of the circle with area .

The density is a constant across the disk, so the CDF at is this same area times . Thus: Then in polar coordinates the density is given by taking partial derivatives:

Once we have , integrate to get the marginals:

Check independence:

In this problem it is feasible to find the marginals directly, without computing the new density, only using some geometric reasoning.

Direct geometric approach

The probability is the area (over ) of a thickened circle with radius and thickness . The circumference of a circle at radius is . So the area of the thickened circle is . So the probability is . This tells us that the marginal probability density is .

The probability is the area (over ) of a thin sector with radius 1 and angle . This area is . So the probability is . This tells us that the marginal probability density is .

These results agree with those of the ‘calculus’ approach above!