Course Landing Page

W14 - Examples

5 min read

Statistical testing cont’d

ML test: Smoke detector

Suppose that a smoke detector sensor is configured to produce when there is smoke, and otherwise. But there is background noise with distribution .

Design an ML test for the detector electronics to decide whether to activate the alarm.

What are the three error probabilities? (Type I, Type II, Total.)

Solution

First, establish the conditional distributions:

Density functions:

The ML condition becomes:

Therefore, is , while is .

The decision rule is: activate alarm when .

Type I error:

Type II error:

Total error:

MAP test: Smoke detector

Suppose that a smoke detector sensor is configured to produce when there is smoke, and otherwise. But there is background noise with distribution .

Suppose that the background chance of smoke is . Design a MAP test for the alarm.

What are the three error probabilities? (Type I, Type II, Total.)

Solution

First, establish priors:

The MAP condition becomes:

Therefore, is , while is .

The decision rule is: activate alarm when .

Type I error:

Type II error:

Total error:

MC Test: Smoke detector

Suppose that a smoke detector sensor is configured to produce when there is smoke, and otherwise. But there is background noise with distribution .

Suppose that the background chance of smoke is . Suppose the cost of a miss is the cost of a false alarm. Design an MC test for the alarm.

Compute the expected cost.

Solution

We have priors:

And we have costs:

(The ratio of these numbers is all that matters in the inequalities of the condition.)

The MC condition becomes:

Therefore, is , while is .

The decision rule is: activate alarm when .

Type I error:

Type II error:

Total error:

PMF of total cost:

Therefore .

Mean square error

Minimal MSE estimate given PMF

Suppose has the following PMF:

12345
0.150.280.260.190.13

Find the minimal MSE estimate of , given that is even. What is the error of this estimate?

Solution

The minimal MSE given is just where .

First compute the conditional PMF:

Therefore:

The error is:

Minimal MSE estimate from joint PDF

Here is the joint PDF of and :

Find the minimal MSE estimate of in terms of .

What is the estimate of when ? When ?

Answer

Estimating on a variable interval

Suppose that and suppose .

(a) Find (b) Find (c) Find

Solution

(a) Find .

We know .

Given , so is uniform on , we have .

(b) Find .

We know .

To compute this function, we calculate a sequence of densities.

We know and . From these we derive the joint distribution :

Now extract the marginal :

Now deduce the conditional :

Then:

So .

(c) Find .

We need all the basic statistics.

because .

.

using the marginal PDF on . (IBP and L’Hopital are needed.)

also using the marginal .

using , namely:

From this we infer and .

Hence:

Thus:

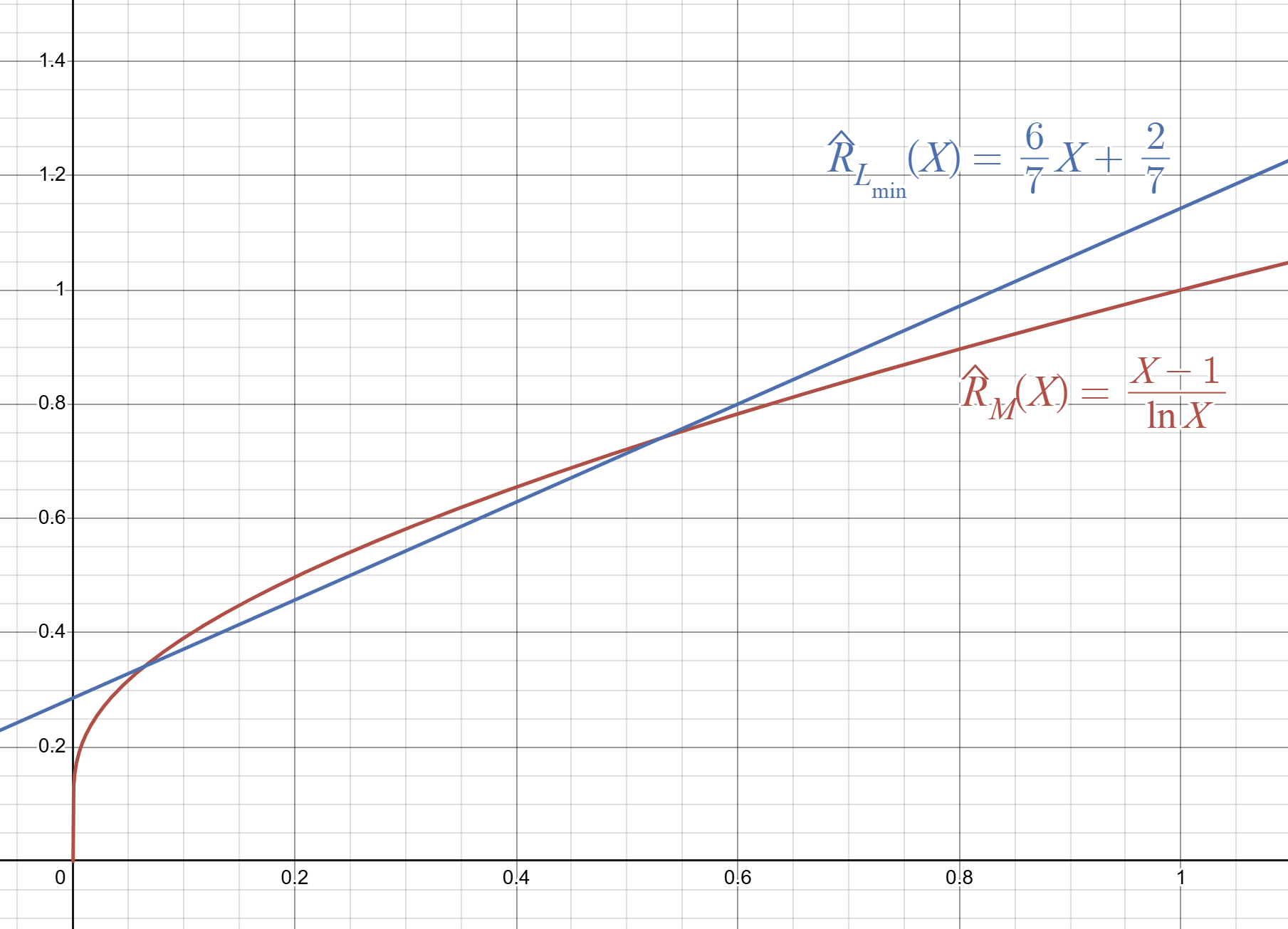
center|400

Line of minimal MSE given joint PDF

Here is the joint PDF of and :

Find the line giving the linear MSE estimate of in terms of .

What is the expected error of this line, ?

What is the estimate of when ? When ?

Answer