Course Landing Page

Week 03 notes

6 min read

Repeated trials

01 Theory

Repeated trials

When a single experiment type is repeated many times, and we assume each instance is independent of the others, we say it is a sequence of repeated trials or independent trials.

The probability of any sequence of outcomes is derived using independence together with the probabilities of outcomes of each trial.

A simple type of trial, called a Bernoulli trial, has two possible outcomes, 1 and 0, or success and failure, or and . A sequence of repeated Bernoulli trials is called a Bernoulli process.

  • Write sequences like for the outcomes of repeated trials of this type.
  • Independence implies
  • Write and , and because these are all outcomes (exclusive and exhaustive), we have . Then:
  • This gives a formula for the probability of any sequence of these trials.

A more complex trial may have three outcomes, , , and .

  • Write sequences like for the outcomes.
  • Label and and . We must have .
  • Independence implies
  • This gives a formula for the probability of any sequence of these trials.

Let stand for the sum of successes in some Bernoulli process. So, for example, “” stands for the event that the number of successes is exactly 3. The probabilities of events follow a binomial distribution.

Suppose a coin is biased with , and is ‘success’. Flip the coin 20 times. Then: Each outcome with exactly 3 heads and 17 tails has probability . The number of such outcomes is the number of ways to choose 3 of the flips to be heads out of the 20 total flips.

The probability of at least 18 heads would then be:

With three possible outcomes, , , and , we can write sum variables like which counts the number of outcomes, and and similarly. The probabilities of events like follow a multinomial distribution.

02 Illustration

Example - Multinomial: Soft drinks preferred

19 - Multinomial: Soft drinks preferred

Reliability

03 Theory

Consider some process schematically with components in series and components in parallel:

400

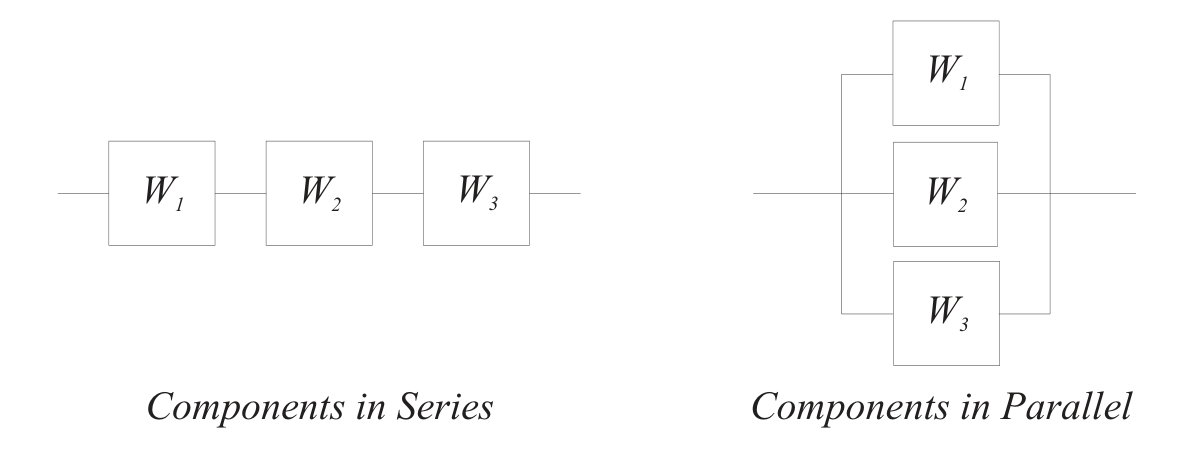
  • Each component has a probability of success or failure.
  • Event indicates ‘success’ of that component (same name).
  • Then is the probability of succeeding.

Success for a series of components requires success of each member.

  • Series components rely on each other.
  • Success of the whole is success of part 1 AND success of part 2 AND part 3, etc.

Failure for parallel components requires failure of each member.

  • Parallel components represent redundancy.
  • Success of the whole is success of part 1 OR success of part 2 OR part 3, etc.

For series components:

For parallel components:

If for all components , then:

  • Series components:
  • Parallel components:

To analyze a complex diagram of series and parallel components, bundle each:

  • pure series set as a single compound component with its own success probability (the product)
  • pure parallel set as a single compound component with its own success probability (using the failure formula)

This is like the analysis of resistors and inductors.

04 Illustration

Example - Series, parallel, series

20 - Reliability: Series, parallel, series

Discrete random variables

05 Theory

Random variable

A random variable (RV) on a probability space is a function .

So assigns to each outcome a number.

  • !!! The word ‘variable’ indicates that the RV outputs numbers.

Random variables can be formed from other random variables using mathematical operations on the output numbers.

Given random variables and , we can form these new ones: Suppose is some particular outcome. Then, for example, is by definition .

Random variables determine events.

  • Given , the event “” is equal to the set
  • That is: the set of outcomes mapped to by
  • That is: the event “ took the value ”

Such events have probabilities. We write them like this:

This generalized to events where lies in some range or set, for example:

The axioms of probability translate into rules for these events.

For example, additivity leads to:

A discrete random variable has probability concentrated at a discrete set of real numbers.

  • A ‘discrete set’ means finite or countably infinite.
  • The distribution of probability is recorded using a probability mass function (PMF) that assigns probabilities to each of the discrete real numbers.
  • Numbers with nonzero probability are called possible values.

PMF

The PMF function for (a discrete RV) is defined by:

for a possible value.

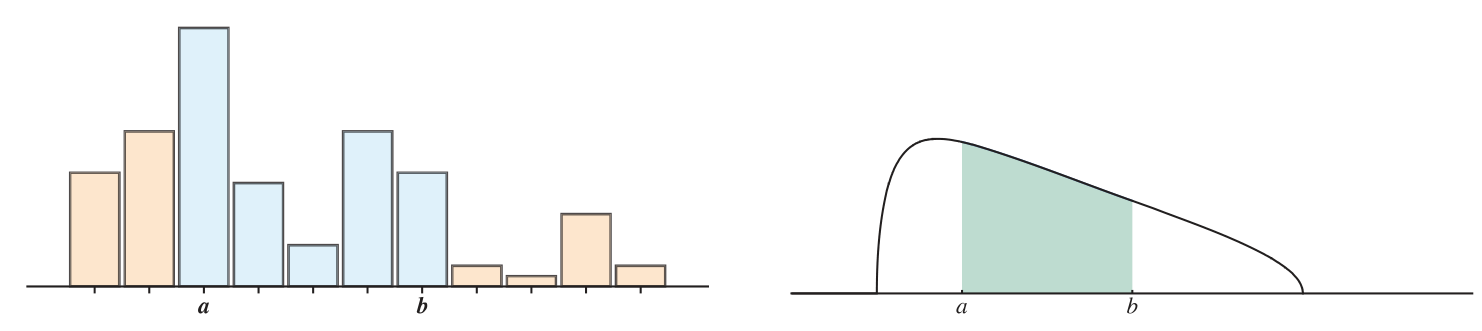
A continuous random variable has probability spread out over the space of real numbers.

  • The distribution of probability is recorded using a probability density function (PDF) which is integrated over intervals to determine probabilities.

PDF

The PDF function for (a CRV) is written for , and probabilities are calculated like this:

500

For any RV, whether discrete or continuous, the distribution of probability is encoded by a function:

CDF

The cumulative distribution function (CDF) for a random variable is defined for all by:

Notes:

  • Sometimes the relation to is omitted and one sees just “.”
  • Sometimes the CDF is called, simply, “the distribution function” because:
  • ! The CDF works equally well for discrete and continuous RVs.
    • Not true for PMF (discrete only) or PDF (continuous only).
    • There are mixed cases (partly discrete, partly continuous) for which the CDF is essential.

The CDF of a discrete RV is always a stepwise increasing function. At each step up, the jump size matches the PMF value there.

From this graph of 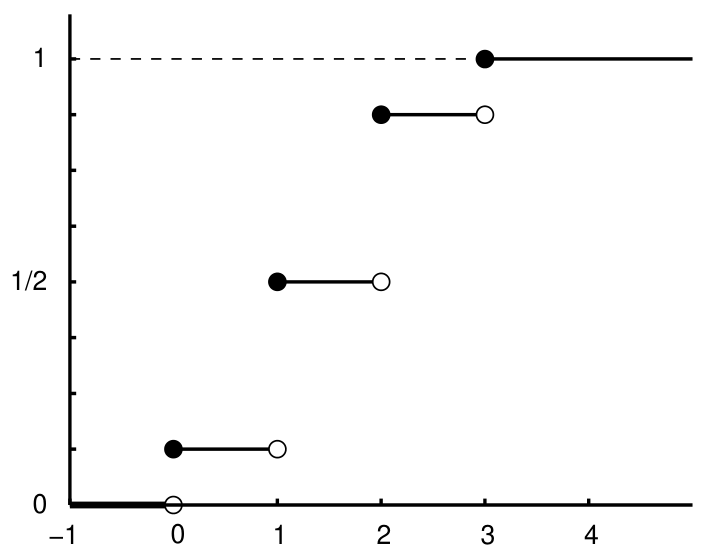: 300

we can infer the PMF values based on the jump sizes:

For a discrete RV, the CDF and the PMF can be calculated from each other using formulas.

PMF from CDF from PMF

Given a PMF , the CDF is determined by: where is the set of possible values of .

Given a CDF , the PMF is determined by:

06 Illustration

Example - PDF and CDF: Roll 2 dice

21 - PDF and CDF: Roll 2 dice

Example - Total heads count; binomial expansion of 1

22 - PMF for total heads count; binomial expansion of 1

Example - Life insurance payouts

23 - Life insurance payouts