Week 10 notes

Expectation for two variables

01 Theory

Expectation for a function on two variables

Discrete case:

Continuous case:

These formulas are not trivial to prove, and we omit the proofs. (Recall the technical nature of the proof we gave for in the discrete case.)

---

Expectation sum rule

Suppose and are any two random variables on the same probability model.

Then:

We already know that expectation is linear in a single variable: .

Therefore this two-variable formula implies:

Expectation product rule: independence

Suppose that and are independent.

Then we have:

---

Extra - Proof: Expectation sum rule, continuous case

Suppose and give marginal PDFs for and , and gives their joint PDF.

Then:

Observe that this calculation relies on the formula for , specifically with .

Extra - Proof: Expectation product rule

02 Illustration

from joint PMF chart

Exercise - Understanding expectation for two variables

Suppose you know only that and .

Which of the following can you calculate?

two ways, and , from joint density

Covariance and correlation

03 Theory

Write and .

Observe that the random variables and are “centered at zero,” meaning that .

Covariance

Suppose and are any two random variables on a probability model. The covariance of and measures the typical synchronous deviation of and from their respective means.

Then the defining formula for covariance of and is:

There is also a shorter formula:

To derive the shorter formula, first expand the product and then apply linearity.

Notice that covariance is always symmetric:

The self covariance equals the variance:

The sign of reveals the correlation type between and :

Correlation	Sign
Positively correlated
Negatively correlated
Uncorrelated

---

Correlation coefficient

Suppose and are any two random variables on a probability model.

Their correlation coefficient is a rescaled version of covariance that measures the synchronicity of deviations:

The rescaling ensures:

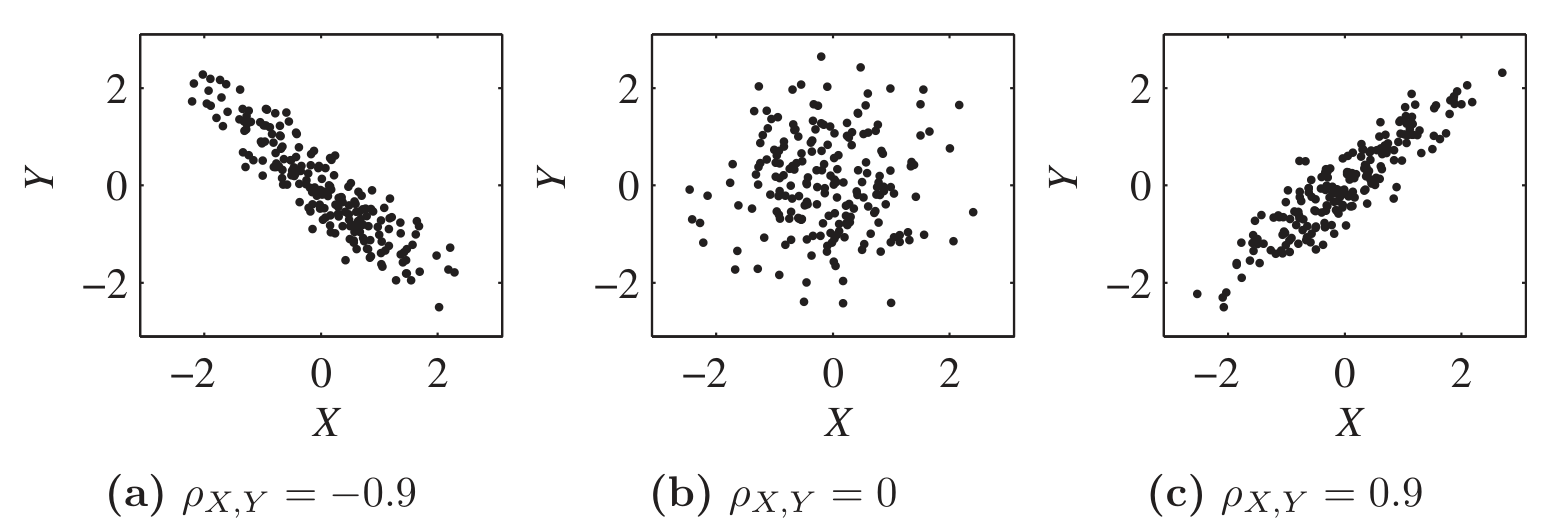
Covariance depends on the separate variances of and as well as their relationship.

Correlation coefficient, because we have divided out , depends only on their relationship.

04 Illustration

Covariance from PMF chart

05 Theory

Covariance bilinearity

Given any three random variables , , and , we have:

Covariance and correlation: shift and scale

Covariance scales with each input, and ignores shifts:

Whereas shift or scale in correlation only affects the sign:

Extra - Proof of covariance bilinearity

Extra - Proof of covariance shift and scale rule

---

Independence implies zero covariance

Suppose that and are any two random variables on a probability model.

If and are independent, then:

Sum rule for variance

Suppose that and are any two random variables on a probability space.

Then:

When and are independent, the formula simplifies to:

Proof: Independence implies zero covariance

The product rule for expectation, since and are independent:

The shorter formula for covariance:

But , so those terms cancel and .

Proof: Sum rule for variance

Proof that

1. Create standardizations:
2. Now and satisfy and .
3. Observe that for any . Variance can’t be negative.
4. Apply the variance sum rule.
   • Apply to and :
   • Simplify:
   • Notice effect of standardization:
   • Therefore .
5. Modify and reapply variance sum rule.
   • Change to :
   • Simplify:

06 Illustration

Exercise - Covariance rules

Simplify:

Exercise - Independent variables are uncorrelated

Let be given with possible values and PMF given uniformly by for all three possible . Let .

Show that and are dependent but uncorrelated.

Hint: To speed the calculation, notice that .

Variance of sum of indicators