Probability
Home

W02 - HW Solutions

01

(1) Use the Law of Total Probability to find .

(2) Use Bayes’ Theorem to find .

(3) Use Bayes’ Theorem to find .

(4) Use Bayes’ Theorem to find .

02

Label the two ‘more qualified’ as A, B, and the three ‘less qualified’ as C, D, E.

9 options have at least one less qualified. 3 options have both less qualified.

Answer

03

Let A be a syntax error and B a logic error.

04

(1) Define events.

Let be the event that she watches it.

Let be the event that the computer is stolen.

We are given the probabilities , , .

We are asked to compute .

(2) Set up formula using Bayes’ Theorem.

(3) Plug in values.

05

(1) Define events.

Let be the event in which you draw the 4-sided die, be the event in which you draw the 6-sided die, and be the event in which you draw the 12-sided die.

We are asked to compute .

(2) Define obvious probabilities.

.

.

.

.

(3) Use Bayes’ Theorem to set up the formula for .

(4) Plug in values and solve.

06

(a) Letters in ways Digits in ways For each 3 letter arrangement, there are 5040 digit arrangements. Total number of ways

(b) Letters in ways Decide the spots for the two 9’s first: Remaining 2 digits in ways Total number of ways:

07

(1) Use inclusion-exclusion principle.

(2) Use the fact that they are mutually independent.

08

(1) Find probabilities for individual events.

.

(2) Compute pairwise probabilities.

The only way and happen is when the second flip is heads and the first and third flip are tails, and when the first and third are heads and when the second is heads. So, .

The only way and happen is when only the third flip is heads or when only the first and second flip are heads. So, .

The only way and happen is when only the first flip is heads or when only the second and third flip are heads. So, .

(3) Disprove mutual independence.

, , and cannot happen simultaneously, so .

09

(a)

(1) Define events.

We define the sample space as .

is the first ball drawn, the second, and the third.

represents the event in which a red ball is drawn, represents the event in which a white ball is drawn, represents the event in which a blue ball is drawn.

(2) Compute .

(b)

(1) We are asked to compute . Use Bayes’ Theorem to set up formula for .

(2) Find probabilities for all relevant combinations.

(3) Plug in values.

10

(a)

If the order matters, then we are dealing with a permutation. We want distinct numbers, so

(b)

If the order matters, then we are dealing with a combination. We want distinct numbers, so

11

(1) Consider how the days are chosen.

Since we just want two days out three given days, it is unordered, so we account for this with the term.

(2) Consider the probability that Wisconsin’s flag is hung on the first two days, and not the third.

The probability that Wisconsin’s flag is hung up is , and the probability it’s any other flag is .

Therefore, the desired probability is .

(3) Combine terms.

12

(1) Define relevant events.

If two balls of different colors are drawn out, then we choose one of each color.

Since order doesn’t matter, our sample space consists of all the ways we choose 2 balls out of 7.

(2) Compute probability.

13

(a)

(b)

14

15

16

(a)

Let be the outcome of the first card, be the outcome of the second card, and denote “hearts”. Since there are 52 cards in a standard deck with 13 of them being hearts, we have

(b)

Similarly to part (a), we have

17

(1) State the inclusion-exclusion principle.

(2) Examine the maximum value of .

We know that .

Given that and , .

(3) Examine the minimum value of .

The minimum value of is the maximum of the individual values.

.

Therefore, .

18

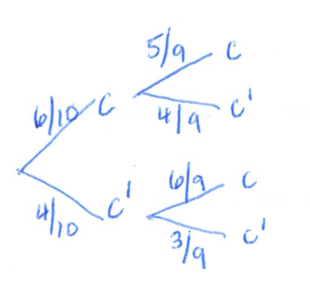
(a) center

Note: gives the wrong answer!

(b)

(c)