Probability
Home

W09 - HW Solutions

01

(1) Start by finding the CDF of :

Let us compute :

Thus, we have that:

(2) Finally, differentiate to find the density :

02

(a)

(1) First, we define the PDF’s and CDF’s of and :

(2) Now:

since, by definition, .

By independence:

Thus, we have:

and thus,

(b)

(1) Similarly, for , we have that . Thus, we have:

by independence. Thus, we have that:

(2) Thus, the density function is given by:

03

(1) Let . We want to find , which we shall do using the convolution formula. Loosely, we have that for acceptable values of a ^7hebc8nd .

(2) First, consider the range of : Since and , we have that . Thus, we need only concern ourselves with the case when .

(3) Now that we have a range for , we must now find acceptable values of . Since both and , we have that . However, , by the condition for the JPDF given above. Thus, .

(4) Similarly, and . Solving the second equation, we have that . Thus, . Since , , . Thus, we can restrict our condition to .

(5) Now that we have bounds, we can finally apply the convolution formula:

(6) We now take cases to deal with the upper bound: when , , and so our upper bound is . If , and , so our upper bound is . Plugging these values in and evaluating, we have our density function:

04

(1) Convolution formula:

The range of is .

(2) Divide into cases:

:

:

:

(Note: there are satisfying this inequality because we assume .)

:

.

(3) Write out piecewise function:

05

(a)

Compute

(b)

Compute .

  • Note that and .

(c)

Compute .

  • Since and are known to be independent, .

(d)

Compute

  • Since , .

06

(1) Define random variables for partitioning the 30 flips into groups of 10.

Let be the number of heads in the first 10 flips.

Let be the number of heads in the middle 10 flips.

Let be the number of heads in the last 10 flips.

Clearly, and are independent.

Note that and .

(2) Compute and

(3) Compute

(4) Compute

Since and , .

Thus,

(5) Compute

(6) Compute .

07

(1) Define indicator variables and

Let denote whether occurs

Let denote whether occurs.

Note that they are independent since and are independent ().

Let .

(2) Compute .

08

(1) Recall the formula for .

Therefore, if , then , and note that .

(2) Compute .

Thus, .

(3) Isolate in the above equation.

Thus, , where .

09

(1) Define random variables to describe the problem.

  • Let to represent the arrival time of the plumber.
  • Let represent the completion time of the sink fix.

(2) Compute

  • This represents the expected time the plumber finishes the job.
  • Thus, we expect the plumber to finish at .

(3) Compute the variance of the finish time.

10

(a)

Compute by integrating the joint PDF.

(b)

Compute .

(c)

Compute

(d)

(1) Compute

(2) Compute .

(e)

(1) Compute

(2) Compute .

(f)

Compute

(g)

Compute .

(h)

Determine independence.

  • Since , we can conclude that and are not independent.

11

(a)

Note that the formula for .

(b)

Compute using the same formula.

(c)

(1) Recall the formula for .

(2) Compute and .

(3) Compute .

(4) Compute .

(d)

(1) Recall the formula for .

(2) Compute and .

(3) Compute and .

(4) Compute

12

(1) Write PDFs:

PDFs of and :

Joint PDF using independence:

(2) CDF of Min:

Write . Then:

(3) Evaluate with formula for :

For :

Therefore:

13

(1) Write PDFs:

PDFs of and :

Joint PDF using independence:

Method 1: CDF first

(2) CDF of sum:

Write . Then:

Plug in .

For :

For :

(3) PDF from CDF:

Method 2: Convolution formula

(2) Convolution:

For :

For :

14

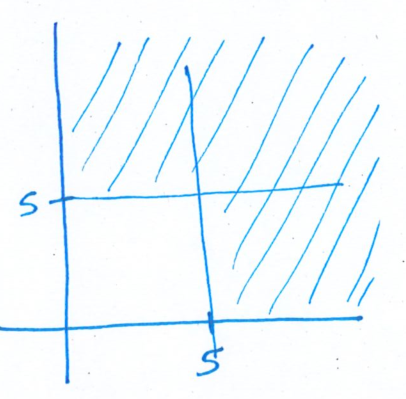
center

15

center

(a) Range of is .

(b)

Alternate:

(c)

16

(b)

17

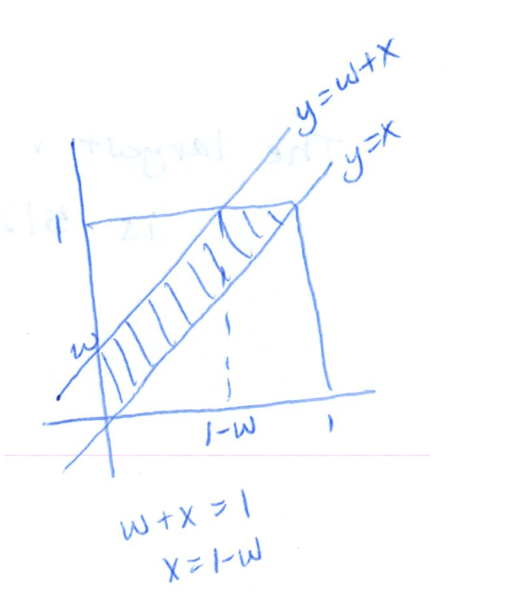
(a) From the sketch, we observe that will be nonnegative. Hence for . Since has a uniform distribution on , for , . We use this fact to find the CDF of . For ,

For and so

The complete CDF can be written as

(b) By taking the derivative, the PDF is

Thus, has an exponential PDF. In fact, since most computer languages provide uniform [ 0,1] random numbers, the procedure outlined in this problem provides a way to generate exponential random variables from uniform random variables.

(c) Since is an exponential random variable with parameter .