Vector Calculus - Packet 04

Surfaces: basic examples

Quadric surfaces are given in as the set of points satisfying a quadratic equation in three variables. The most general form of equation is:

After applying a rigid motion to , any such equation can be converted to one of these simpler equations:

The surfaces satisfying Equation (1) include spheres, cones, cylinders, ellipsoids, and hyperboloids. The surfaces satisfying Equation (2) include elliptic paraboloids and hyperbolic paraboloids.

The surface type can be deduced from the coefficients or .

One way to study equations of quadrics is to consider their traces, which are conic sections in two variables given by setting the third variable constant. A trace is the intersection of the quadric surface with the plane determined by the constant variable.

Exercise 04A-01

Translating away linear terms of a quadric

Show how you can eliminate the linear part from the general equation of a quadric by completing squares.

Rotating away cross-variable terms of a quadric

Libretext link for an explanation of how to eliminate cross-variable terms by applying rotations.

Spheres

The general equation of a sphere in with center at and radius is given by:

This equation is justified by the generalized Pythagorean theorem for three dimensions.

Spherical coordinates parametrize a sphere at radius . The angle is the standard angle in the -plane, and the angle measures declination from the north pole. These coordinates may be converted to standard coordinates:

Warning

Note that give coordinates for points in , but the numbers are not vector components. Do not perform vector operations componentwise on !

Cylinders generalized

A simple cylinder is a tube extended in the 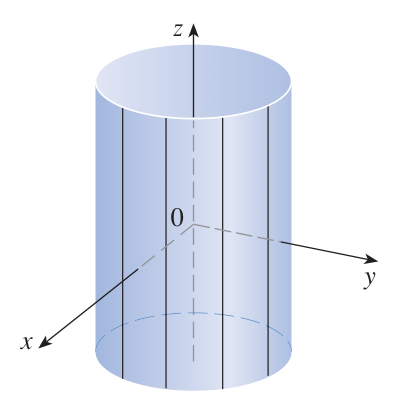-coordinate with a circle for each -cross-section. No constraint on the -coordinate is needed, and the -coordinates satisfy the equation of a circle: .

More generally, the set of points 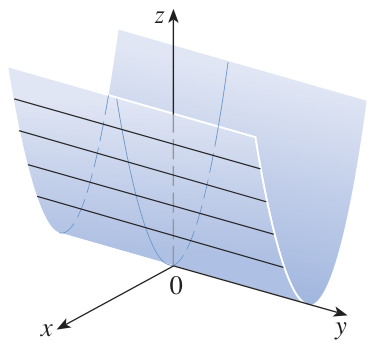satisfying an equation in terms of only two variables gives a generalized cylinder, extended in the coordinate of the missing variable. For example, gives a parabolic cylinder extended in the -coordinate: For any cylindrical surface, it is possible to find new coordinates in which the surface is defined using only two of them.

Note that quadric surfaces written with two variables are generalized cylinders, but most generalized cylinders are not quadratic!

Exercise 04A-02

Describe surfaces

Describe the surface accurately using as few words as possible:

• (a)
• (b)
• (c)
• (d)
• (e)

Exercise 04A-03

Describe surfaces

Describe the surface accurately using as few words as possible:

• (a)
• (b)
• (c)
• (d)
• (e)

Exercise 04A-04

Surfaces: rectangular to spherical coordinates

Find an equation in spherical coordinates of the form for the following surfaces given in rectangular coordinates:

• (a)
• (b)
• (c)
• (d)

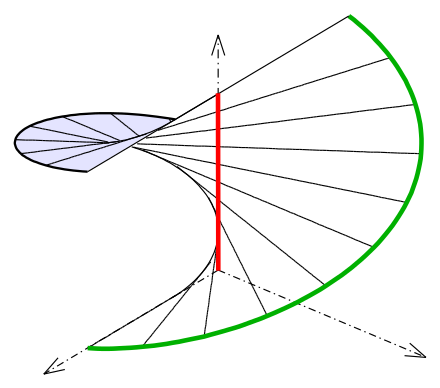
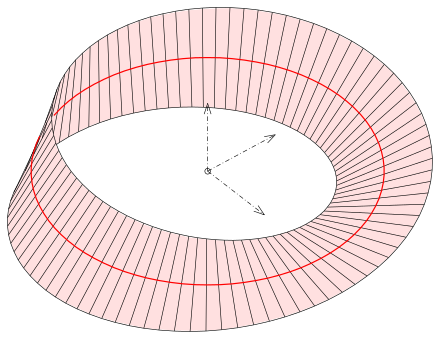
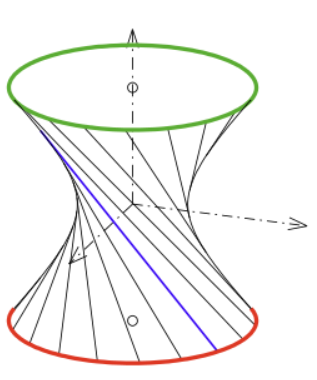
Ruled surfaces

Generalized cylinders are examples of ruled surfaces, which are surfaces created by the smooth motion through space of a straight line. For generalized cylinders, the lines must remain parallel, i.e. the motion must be perpendicular to the lines.

Other ruled surfaces that are not generalized cylinders: Helicoid:

Mobius strip:

Hyperboloid:

Quadrics: ellipsoids

Ellipsoids are quadrics surfaces of type with and .

Under these conditions, the quadric equation can be rewritten into a more expressive form:

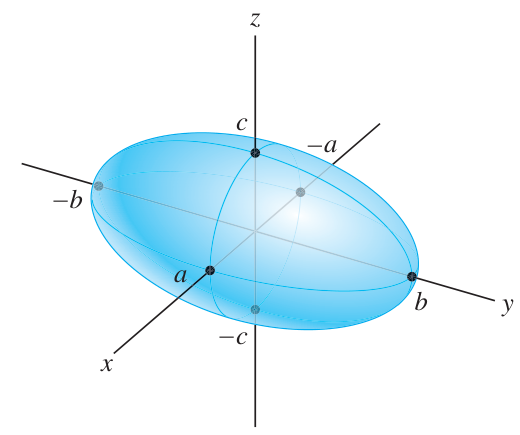
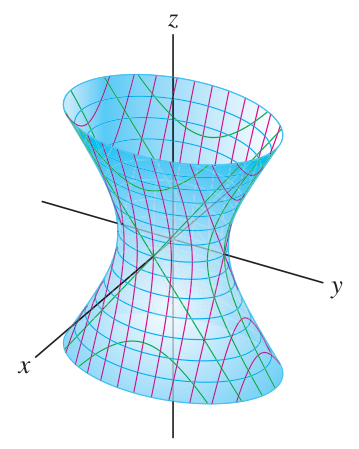
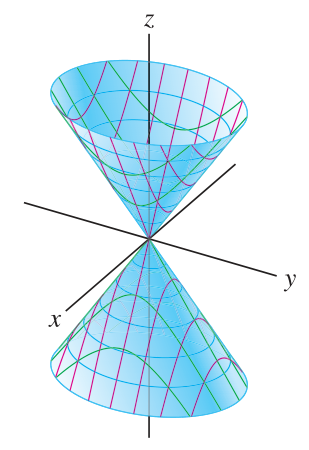
As with an ellipse, the constants determine the three axis lengths of the ellipsoid. When , the ellipsoid is actually a sphere.

Quadrics: hyperboloids

Hyperboloids are quadric surfaces of type with one of less than , and the other two greater.

By exchanging the roles of and rewriting, we can assume the equation takes the form:

There are three kinds of hyperboloids: cones, hyperboloids of one sheet, and hyperboloids of two sheets. They are given by equations with , , and , respectively.

One-sheeted paraboloids include a circle at , which is possible because . Shrinking shrinks the circle at until it is a point at (creating a cone, or more descriptively, a double-cone), and when goes negative, the surface does not exist at .

:

:

:

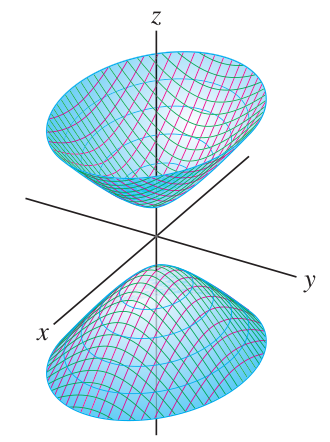
Quadrics: paraboloids

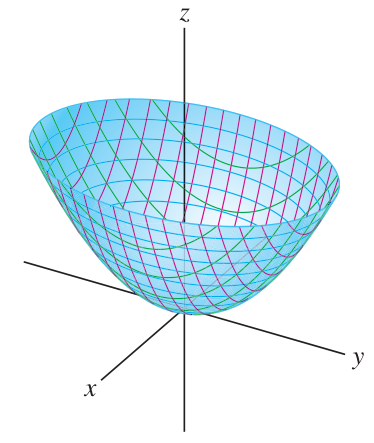
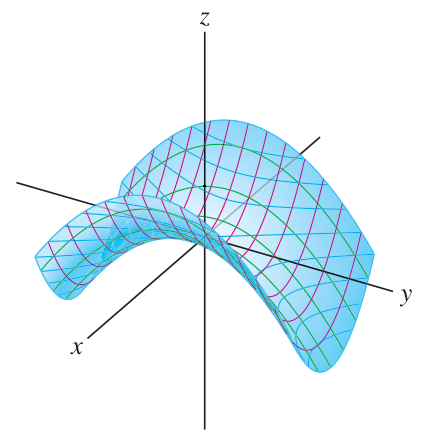
Paraboloids are quadric surfaces of type . For this type, , so we may divide by and thereby assume . We can rewrite the general form:

The paraboloid is elliptic when both signs are plus (opening up) or minus (opening down). The paraboloid is hyperbolic when the signs are opposite.

Elliptic and hyperbolic paraboloids are often useful to illustrate optimization methods. A paraboloid has a horizontal tangent plane at the bottom (both signs positive), or the top (both negative), or the saddle point (opposite signs).

:

:

Exercise 04A-05

Hyperboloid with circular traces

Suppose a hyperboloid is such that every intersection with a horizontal plane is a circle. Give a simplified form of the general equation for such a surface.

 

 

Problems due 16 Sep 2023, 8:00pm

Problem 04-01

Hyperbolic paraboloids are ruled

Suppose that lies on the hyperbolic paraboloid . Show that the lines given parametrically by the equations and both lie completely within the paraboloid. (Therefore this paraboloid is a ruled surface.)

Problem 04-02

Quadric translation to standard form

Convert the following two general equations of quadrics into standard form. Classify the surfaces they determine.

• (a)
• (b)