Due date: Sunday 1/18, 11:59pm
Shells
01
02
Link to originalShells volume - set up integrals, both axes
Consider the region in the first quadrant bounded by the lines
and , and the curve . Set up integrals to find the volumes of the solids obtained by revolving this region about (i) the
-axis, and (ii) the -axis. (No need to evaluate the integrals in this problem.)
Solution
Solutions - 0030-02
You can set up each integral using disks/washers or using shells.
(1) Using washers, obtain:
Using shells, obtain:
(2) Using disks, obtain:
Using shells, obtain:
Link to original
02
03
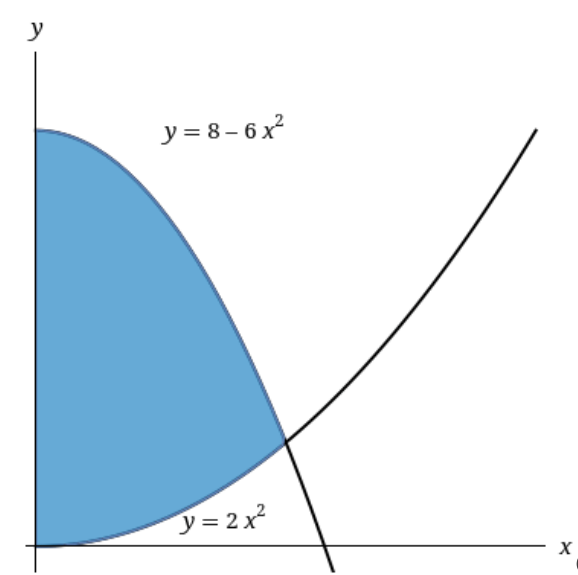
Link to originalShells volume - shells v. washers
Consider the region in the
-plane, in the first quadrant, bounded by the -axis on the left, by on the top, and on the bottom.
A 3D solid is given by revolving this region around the
-axis. (a) Find the volume of the solid using the method of shells.
(b) Attempt to find the volume of the solid using the method of washers/disks. Why is this harder? (TWO reasons!)
Solution
Solutions - 0030-03
(a)
(1) Write down shells formula:
(2) Define the cross section region:
Bounded above by
. Bounded below by . Bounded left by
. Bounded right by intersection at line .
(3) Define
and and :
(4) Plug into shells formula and compute:
(b)
(1) Write down washers formula using
:
(2) Rewrite bounding equations in terms of
:
(3) Determine region boundary data:
Bounded above by
. Bounded below by . Intersection at .
(4) Determine
in two components, with the dividing line: Note that
for both regions. These are disks.
(5) Compute the integral:
(6) Why are shells preferable?
Link to original
- Only need one integral.
- Don’t need to rewrite boundary equations in terms of
.
IBP
03
03
Link to originalIntegration by parts - A and L
Compute the integral:
Solution
Solutions - 0010-03
(1) Select
and considering LIATE:
(2) Apply IBP formula
: Link to original
04
04
Link to originalIntegration by parts - A and E
Compute the integral:
Solution
Solutions - 0010-04
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral: Link to original
05
05
Link to originalIntegration by parts - A and I
Compute the integral:
Solution
Solutions - 0010-05
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral:
(3) Perform
-sub with and :
(4) Insert result in Exp. (A):
Note B: We can change
Link to originalto because the inner expression is never negative.
06
06
Link to originalIntegration by parts - E and T, “breaking the circle”
Compute the integral:
You should perform IBP twice, find an equation, and use algebra to solve it (“breaking the circle”) for the desired integral.
Solution
Solutions - 0010-06
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral: Therefore:
(3) Repeat. Select
and considering LIATE:
(4) Apply IBP formula
and compute integral:
(5) Now insert in Eqn. A:
Introduce notational label:
Now use this label in Eqn. A and solve for
: Link to original