W13 - HW Solutions

01

(a) From the first equation, .

Plug that in for in :

The sketched curve should be the portion of the line with .

---

(b)

For this one, best not to solve for . Instead, notice the trig identity:

Therefore the points on the curve satisfy the equation . Solve this for the function:

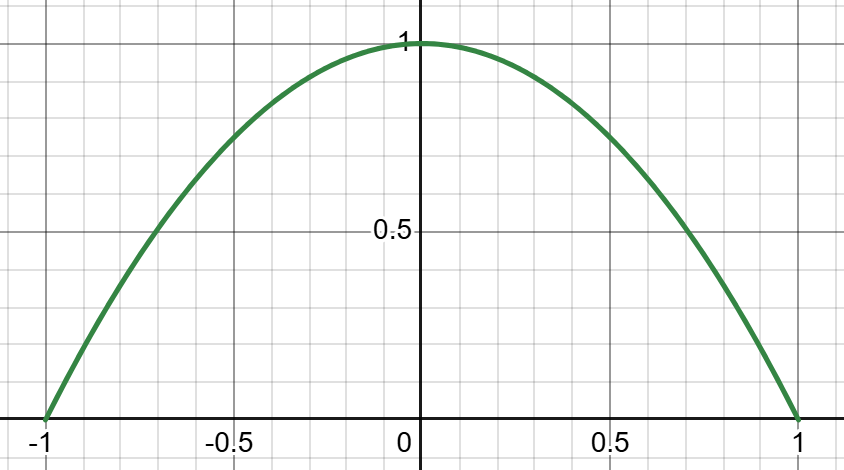
02

Find a formula for the slope of the tangent line:

Solve for the where :

03

Derivative functions:

Slope:

Second derivative:

At :

04

(a)

Observe that and implies .

Therefore, all points on the curve satisfy and we set .

Since and covers the entire real line , the parametric curve is the entire line .

---

(b)

Observe that and implies . Again, all points on the curve satisfy and so .

However, this time implies , and the entire range of is possible (set ) to find an inverse.

So the image of this parametric curve is for , and the origin is omitted.

05

(a)

First choose a function , then set to ensure the equation is satisfied.

When choosing , we want to cover the whole domain of which is . We also need to satisfy the initial condition.

Start by trying :

But then . Since we should have . We can arrange for this by setting and solving for :

Therefore we define . Then:

So we use:

---

(b)

Same method but different condition:

Therefore we define . Then:

So we use:

06

First derivative:

Second derivative:

This is positive if-and-only-if . (Numerator always positive, denominator same sign as .) So:

07

Derivatives:

Arclength: