Calculus II
Home

W14 - HW Solutions

01

(a)

Q1, SAFE, .

(b)

Q1, SAFE, .

(c)

Q2, UNSAFE, and we add to this angle.

(d)

Q2, UNSAFE, (use 30-60-90 triangle) and we add to this angle.

02

(a)

(b)

Use and therefore:

So:

This is a circle centered at with radius .

(c)

Using and :

Note: This assumes that .

03

Observe that this parametric curve is a circle centered at with radius . So we expect vertical tangents at and horizontal tangents at .

Treat as the parameter. We always have . This equals here because . Since we can further simplify to .

Then .

Also .

To find vertical tangents, solve for :

Check that is not also zero at these points, else they would be stationary points:

Now find the Cartesian coordinates for these points:

To find the horizontal tangents, solve for :

Check that is not also zero at these points, else they would be stationary points:

Now find the Cartesian coordinates for these points:

04

(a)

(b)

Method 1:

First compute and . Then and .

Method 2:

Observe . Then , and obtain the answer.

(c)

(d)

05

(a) (b) (c)

(a)

Insert and :

(b)

(c)

06

(a)

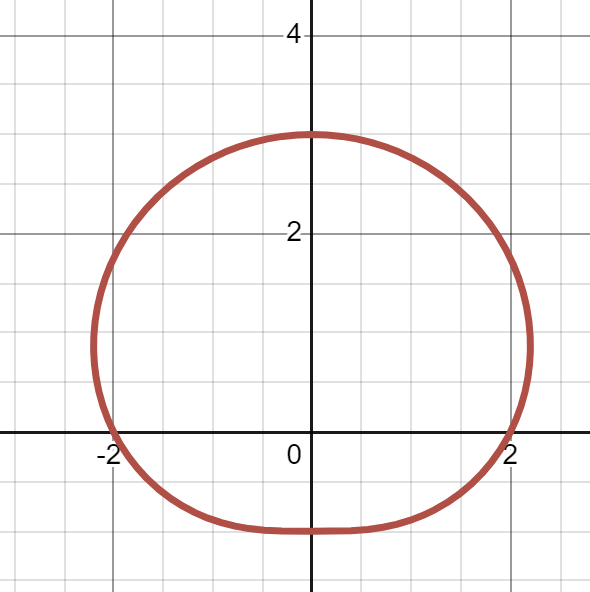
center

(b)

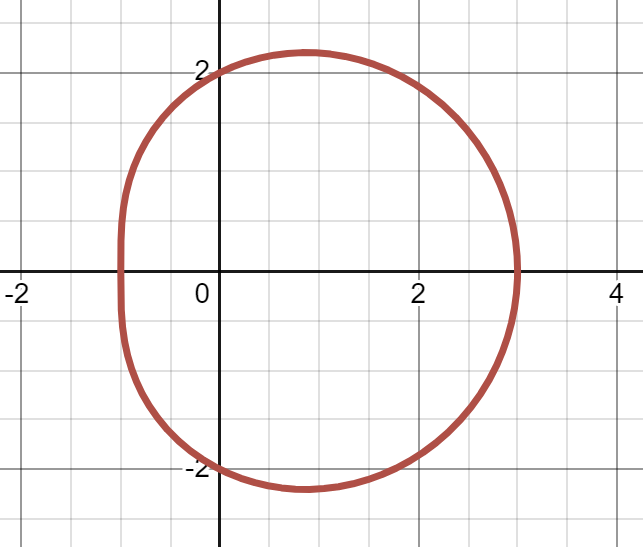
center

(c)

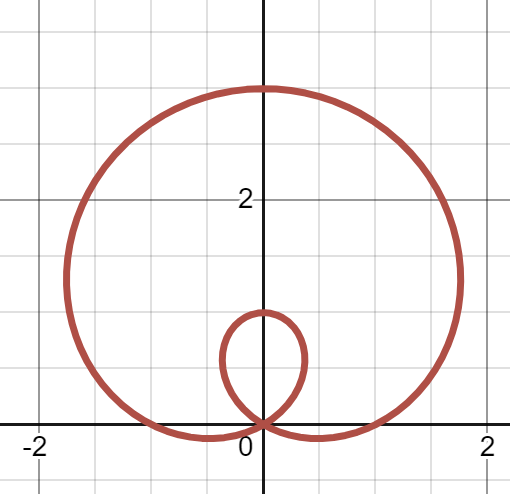
center

(d)

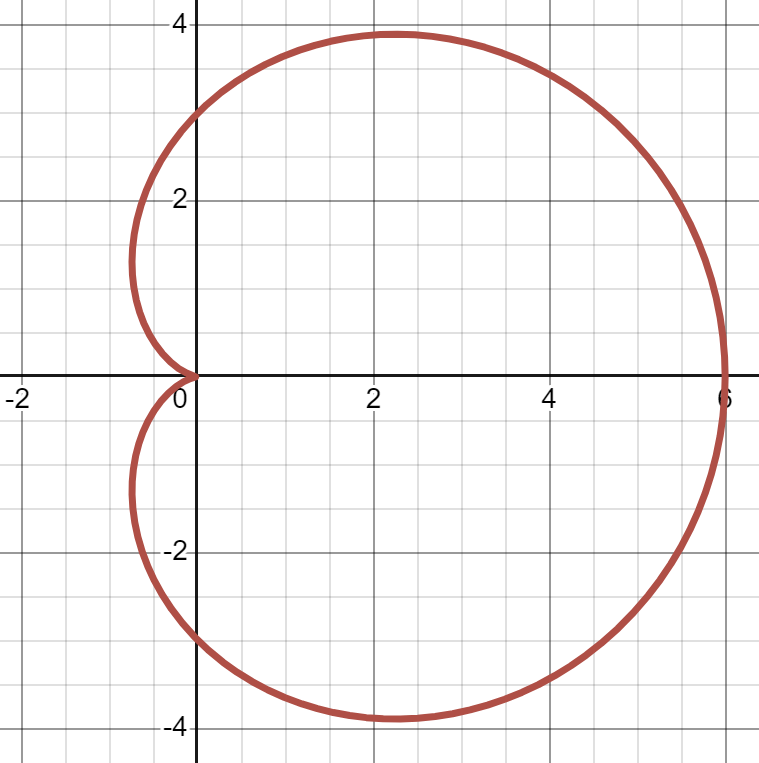
center

07

(a)

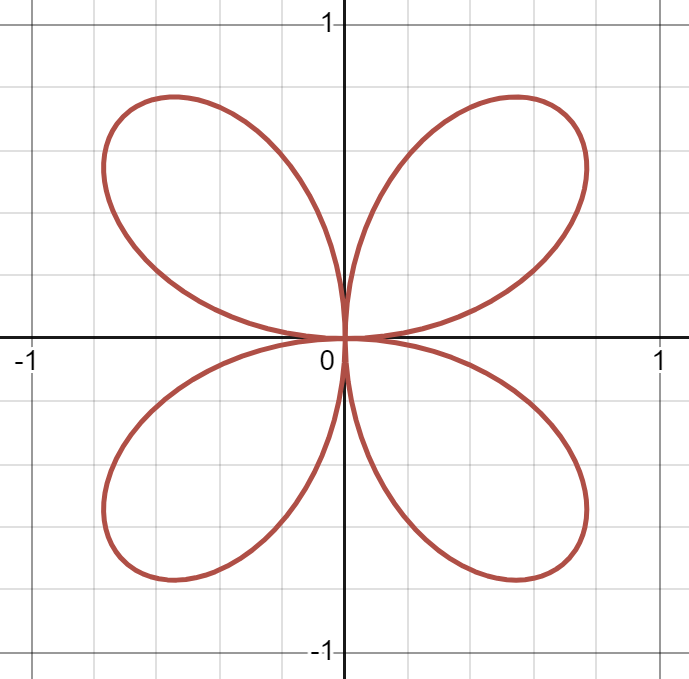
center

Numbers should be placed on the loops, 1, 2, 3, 4, starting in Q1 and going clockwise.

(b)

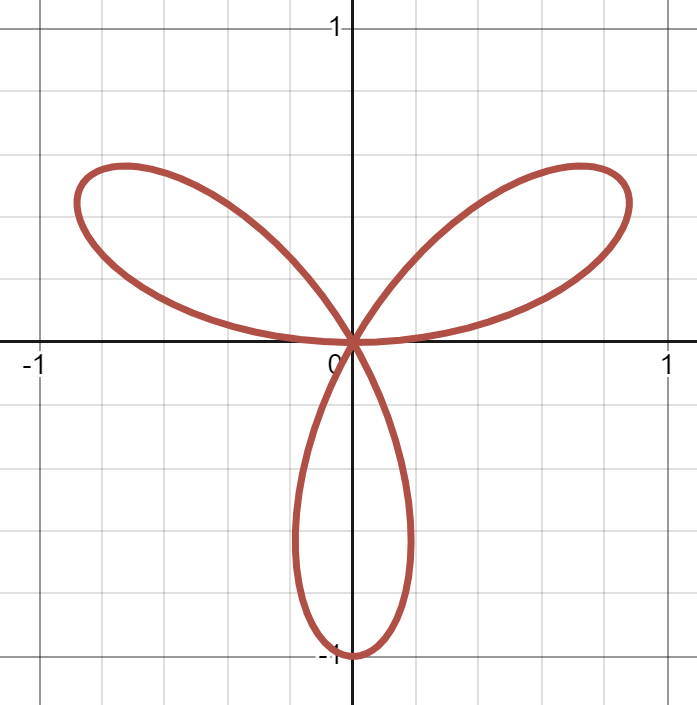
center

Numbers should be placed on the loops, 1, 2, 3, starting in Q1 and going clockwise.

(c)

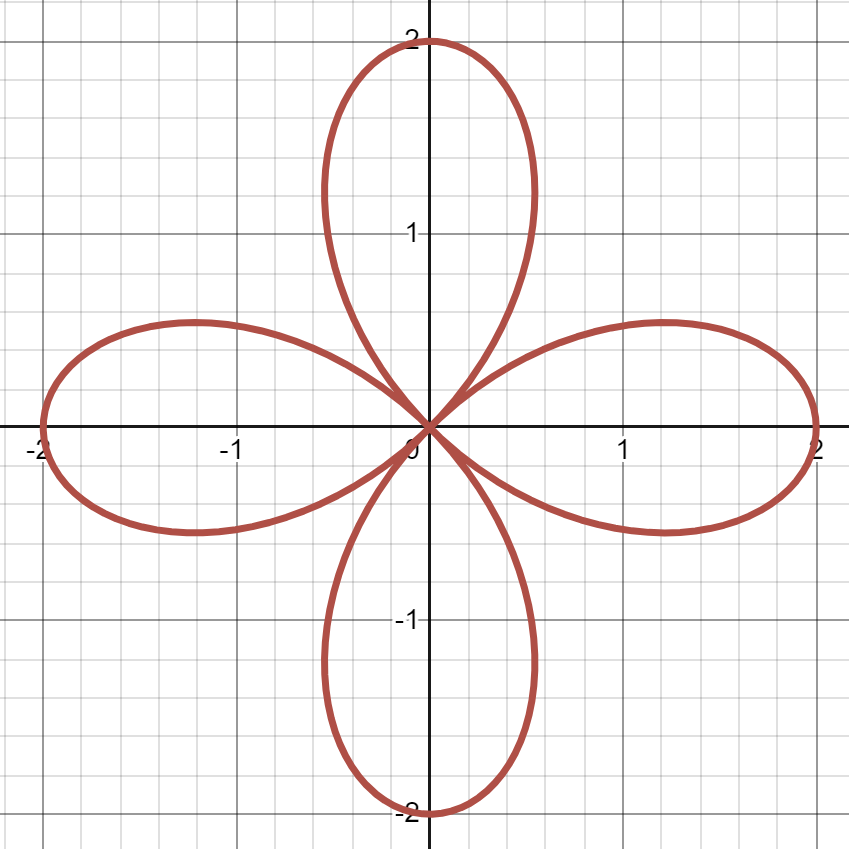
center

Numbers should be placed on the loops, 1, 2, 3, 4, starting on the -axis and going clockwise.

08

Derivatives:

Speed function:

Now we minimize this function as in Calc I.

Method 1:

Differentiate:

This equals zero if-and-only-if the numerator equals zero (assuming the denominator is not zero there):

Since is negative for and positive for , we may deduce that is the time of the minimal value of . So:

Method 2:

Instead of differentiating , we can look at its square , since the minimum of this will occur at the same time as the minimum of (because is a monotone increasing function). But becomes , and the rest of the solution proceeds as in Method 1.

09

(a)

One arch is formed from the range .

Compute :

Therefore .

Now recall a power-to-frequency formula, and use it in reverse:

Therefore:

(b)